题目内容
20.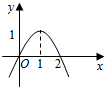 已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.
已知f(x)=ax3+bx2+c,其导函数f′(x)的图象如图所示,则函数f(x)取得极小值时x的值是0.
分析 由图象得到函数f(x)的单调区间,从而求出函数的极小值点.
解答 解:由图象得:在(-∞,0),(2,+∞)上,f′(x)<0,
在(0,2)上,f′(x)>0,
∴函数f(x)在(-∞,0),(2,+∞)递减,在(0,2)递增,
∴f(x)极小值=f(0),
故答案为:0.
点评 本题考查了函数的单调性,考查导数的应用,是一道基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.已知全集U={0,1,2,3,4,5,6},集合A={0,3,5},集合B={2,4,5},则(∁UA)∩B为( )
| A. | {2,4} | B. | {2,6} | C. | {0,1,3} | D. | {2,4,6} |
5.y=x2+2在x=1处的导数为( )
| A. | 2x | B. | 2 | C. | 2+△x | D. | 1 |
9.周长为1,圆心角为1rad的扇形的面积等于( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{18}$ |