题目内容
【题目】已知函数f(x)=cosx(![]() sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移
sinx-cosx)+m(m∈R),将y=f(x)的图象向左平移![]() 个单位后得到g(x)的图象,且y=g(x)在区间[
个单位后得到g(x)的图象,且y=g(x)在区间[![]() ]内的最小值为
]内的最小值为![]() .
.
(1)求m的值;
(2)在锐角△ABC中,若g(![]() )=
)=![]() ,求sinA+cosB的取值范围.
,求sinA+cosB的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)根据二倍角公式化简![]() ,利用平移规律得出
,利用平移规律得出![]() 的解析式,根据最小值列方程求出
的解析式,根据最小值列方程求出![]() ;
;
(2)根据条件求出![]() ,用
,用![]() 表示出
表示出![]() ,化简
,化简![]() 得出关于
得出关于![]() 函数,根据
函数,根据![]() 的范围得出正弦函数的性质得出
的范围得出正弦函数的性质得出![]() 的范围.
的范围.
(1)f(x)=![]() sinxcosx-cos2x+m=
sinxcosx-cos2x+m=![]() sin2x-cos2x+m-=sin(2x-)+m-,
sin2x-cos2x+m-=sin(2x-)+m-,
∴g(x)=sin[2(x+)-]+m-=sin(2x+)+m-,
∵x∈[,],∴2x+∈[![]() ,
,![]() ],
],
∴当2x+=![]() 时,g(x)取得最小值+m-=m,
时,g(x)取得最小值+m-=m,
∴m=![]() .
.
(2)∵g()=sin(C+)+![]() -=-+
-=-+![]() ,
,
∴sin(C+)=![]() ,
,
∵C∈(0,),∴C+∈(,![]() ),
),
∴C+=,即C=.
∴sinA+cosB=sinA+cos(![]() -A)
-A)
=sinA-![]() cosA+sinA
cosA+sinA
=sinA-![]() cosA
cosA
=![]() sin(A-).
sin(A-).
∵△ABC是锐角三角形,∴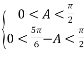 ,
,
解得![]() ,
,
∴A-∈(,),
∴<sin(A-)<![]() ,
,
∴![]() <
<![]() sin(A-)<,
sin(A-)<,
∴sinA+cosB的取值范围是(![]() ,).
,).

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目