Question

【题目】已知抛物线，点M(m, 0)在x轴的正半轴上，过M点的直线与抛物线 C相交于A，B两点，O为坐标原点.

(1) 若m=l，且直线的斜率为1，求以AB为直径的圆的方程；

(2) 是否存在定点M，使得不论直线绕点M如何转动， 恒为定值？

Answer 1

【答案】（1）. (2)存在定点M(2, 0).

【解析】试题分析：（I）由题意得M（1，0），直线l的方程为y=x﹣1与抛物线方程联立，利用韦达定理，可得圆心坐标与圆的半径，从而可得圆的方程；

（II）若存在这样的点M，使得为定值，直线l：x=ky+m与抛物线方程联立，计算|AM|，|BM|，利用恒为定值，可求点M的坐标．

试题解析：

（1）当m=1时，M(1，0)，此时，点M为抛物线C的焦点，

直线的方程为y=x-1，设，联立，

消去y得， ，∴， ，

∴圆心坐标为(3, 2).

又，∴圆的半径为4，

∴圆的方程为.

(2)由题意可设直线的方程为，则直线的方程与抛物线联立，

消去x得： ，则， ，

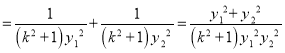
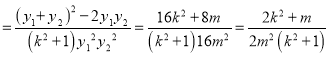
对任意恒为定值，

于是m=2，此时.

∴存在定点M(2, 0)，满足题意.