题目内容
定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”。现有定义在( )
(-∞,0)∪(0,+∞)上的如下函数:①f(x)=x²;②f(x)=2x;③ ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
| A.①② | B.①③ | C.③④ | D.②④ |
B
解析试题分析:等比数列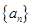 中,设公比为
中,设公比为 ,
,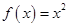 中
中
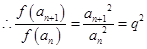 是等比数列,
是等比数列, 中
中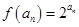
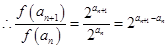
不是常数,不是等比数列,综上①为“保等比数列函数”②不是,结合选项可知选B
考点:等比数列的判定
点评:要判定一个数列是否为等比数列,通常利用定义:看相邻两项之比是否为常数

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知数列{an}的通项公式 ,则
,则 =( )
=( )
| A.2012 | B.2013 | C.2014 | D.2015 |
在函数y=f(x)的图象上有点列(xn,yn),若数列{xn}是等差数列,数列{yn}是等比数列,则函数y=f(x)的解析式可能为( )
| A.f(x)=2x+1 | B.f(x)=4x2 |
| C.f(x)=log3x | D.f(x)= x x |
已知等比数列 中,公比
中,公比 若
若 则
则 有( )
有( )
| A.最小值-4 | B.最大值-4 | C.最小值12 | D.最大值12 |
已知数列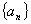 的
的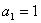 ,且
,且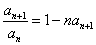 ,则此数列
,则此数列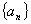 的通项公式为( )
的通项公式为( )
A.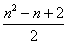 | B.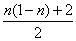 |
C.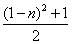 | D.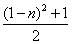 或 或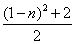 |
1202年,意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系: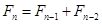 (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则 的值为( )
的值为( )
| A.13 | B.21 | C.34 | D.55 |
已知数列 ,
, ,
, ,且
,且 ,则数列的第五项为( )
,则数列的第五项为( )
A. | B. | C. | D. |
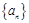 的各项均为正数,且
的各项均为正数,且 ,则
,则








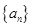 中,
中,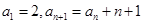 ,则通项
,则通项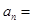 ___________.
___________.