题目内容
1202年,意大利数学家斐波那契在他的书中给出了一个关于兔子繁殖的递推关系: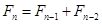 (
( ),其中
),其中 表示第
表示第 个月的兔子的总对数,
个月的兔子的总对数, ,则
,则 的值为( )
的值为( )
| A.13 | B.21 | C.34 | D.55 |
B
解析试题分析:∵ ,∴
,∴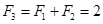 ,∴
,∴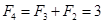 ,
,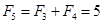 ,
,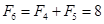 ,
,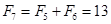 ,∴
,∴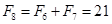 ,故选B
,故选B
考点:本题考查了数列的通项
点评:熟练运用递推式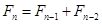 求值是解决此类问题的关键,属基础题
求值是解决此类问题的关键,属基础题

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
已知正项等比数列 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则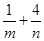 的最小值为( )
的最小值为( )
| A.9 | B. | C. | D. |
已知-7,a1,a2,-1四个实数成等差数列,-4,b1,b2,b3,-1五个实数成等比数列,则 = ( )
= ( )
| A.1 | B.-1 | C.2 | D.±1 |
定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”。现有定义在( )
(-∞,0)∪(0,+∞)上的如下函数:①f(x)=x²;②f(x)=2x;③ ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
| A.①② | B.①③ | C.③④ | D.②④ |
数列 则
则 是该数列的( )
是该数列的( )
| A.第6项 | B.第7项 | C.第8项 | D.第9项 |
一个赛跑机器人有如下特性:
(1)步长可以人为地设置成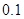 米,
米,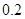 米,
米,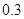 米,…,
米,…,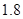 米或
米或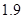 米;
米;
(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;
(3)当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒.
则这个机器人跑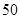 米(允许超出
米(允许超出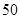 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.
A.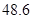 秒 秒 | B.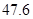 秒 秒 | C.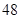 秒 秒 | D.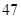 秒 秒 |
已知数列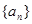 的通项公式为
的通项公式为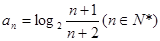 ,设其前n项和为Sn,
,设其前n项和为Sn,
则使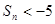 成立的自然数n( )
成立的自然数n( )
| A.有最大值63 | B.有最小值63 |
| C.有最大值32 | D.有最小值32 |
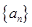 的各项均为正数,前
的各项均为正数,前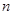 项和为
项和为 ,对于任意的
,对于任意的 ,
,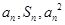 成等差数列,设数列
成等差数列,设数列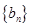 的前
的前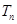 ,且
,且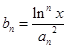 ,则对任意的实数
,则对任意的实数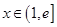 (
(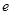 是自然对数的底)和任意正整数
是自然对数的底)和任意正整数