题目内容
已知数列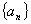 的
的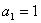 ,且
,且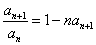 ,则此数列
,则此数列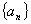 的通项公式为( )
的通项公式为( )
A.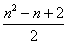 | B.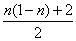 |
C.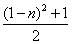 | D.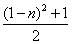 或 或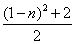 |
A
解析试题分析:由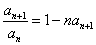 可得,
可得,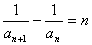 ,令
,令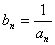 ,则
,则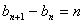 ,因此
,因此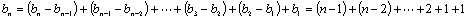
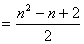 ,故选A.
,故选A.
考点:本题主要考查等差数列的通项公式。
点评:中档题,利用数列的递推公式,考查项的倒数之间的关系,确定得到等差数列。

练习册系列答案
相关题目
已知数列 满足:
满足: ,
, ,若
,若 ,
, ,且数列
,且数列 的单调递增数列,则实数
的单调递增数列,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
若数列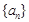 满足:存在正整数
满足:存在正整数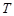 ,对于任意正整数
,对于任意正整数 都有
都有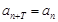 成立,则称数列
成立,则称数列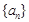 为周期数列,周期为
为周期数列,周期为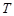 . 已知数列
. 已知数列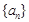 满足
满足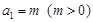 ,
,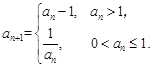
则下列结论中错误的是( )
A.若m=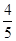 ,则a5=3 ,则a5=3 |
| B.若a3=2,则m可以取3个不同的值 |
C.若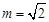 ,则数列 ,则数列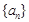 是周期为 是周期为 的数列 的数列 |
D.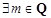 且 且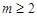 ,数列 ,数列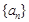 是周期数列 是周期数列 |
已知数列 为等差数列,
为等差数列,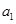 +
+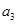 +
+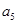
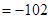 ,
,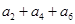
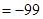 ,以
,以 表示
表示 的前
的前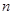 项和,则使得
项和,则使得 达到最小值的
达到最小值的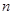 是( )
是( )
| A.37和38 | B.38 | C.37 | D.36和37 |
定义在(-∞,0)∪(0,+∞)上的函数f(x),如果对于任意给定的等比数列{an},{f(an)}仍是等比数列,则称f(x)为“保等比数列函数”。现有定义在( )
(-∞,0)∪(0,+∞)上的如下函数:①f(x)=x²;②f(x)=2x;③ ;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
;④f(x)="ln|x" |。则其中是“保等比数列函数”的f(x)的序号为 ( )
| A.①② | B.①③ | C.③④ | D.②④ |
已知数列 成等差数列,
成等差数列,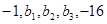 成等比数列,则
成等比数列,则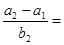 ( )
( )
A.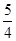 | B.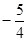 | C.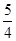 或 或 | D. |
一个赛跑机器人有如下特性:
(1)步长可以人为地设置成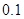 米,
米,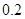 米,
米,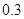 米,…,
米,…,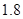 米或
米或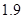 米;
米;
(2)发令后,机器人第一步立刻迈出设置的步长,且每一步的行走过程都在瞬时完成;
(3)当设置的步长为 米时,机器人每相邻两个迈步动作恰需间隔
米时,机器人每相邻两个迈步动作恰需间隔 秒.
秒.
则这个机器人跑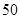 米(允许超出
米(允许超出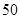 米)所需的最少时间是【 】.
米)所需的最少时间是【 】.
A.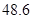 秒 秒 | B.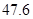 秒 秒 | C.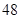 秒 秒 | D.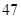 秒 秒 |
数列 满足
满足 ,且对任意的
,且对任意的
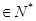 都有:
都有: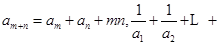
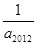 等于 ( )
等于 ( )
A. | B.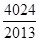 | C.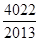 | D.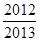 |
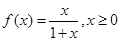 ,若
,若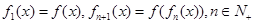 ,则
,则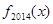 的表达式为________.
的表达式为________.