题目内容
已知函数
(1)用定义证明 在
在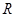 上单调递增;
上单调递增;
(2)若 是
是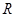 上的奇函数,求
上的奇函数,求 的值;
的值;
(3)若 的值域为D,且
的值域为D,且 ,求
,求 的取值范围.
的取值范围.
(1)设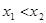 且
且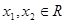
则
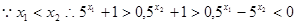
 即
即
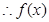 在
在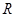 上单调递增 ;
上单调递增 ;
(2) ;(3)
;(3)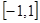 .
.
解析试题分析:(1)在定义域内任取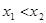 ,证明
,证明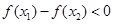 ,即
,即 ,所以
,所以 在
在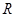 上单调递增;(2)因为,
上单调递增;(2)因为, 是
是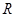 上的奇函数,所以
上的奇函数,所以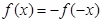 ,即
,即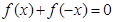 ,代入表达式即可得
,代入表达式即可得 ;(3)可求得
;(3)可求得 的值域
的值域 ,由
,由 可得不等式
可得不等式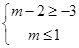 ,所以
,所以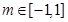 .
.
试题解析:(1)设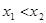 且
且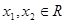 1分
1分
则 3分
3分
 即
即 5分
5分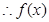 在
在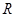 上单调递增 6分
上单调递增 6分
(2) 是
是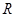 上的奇函数
上的奇函数 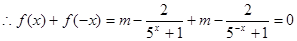 8分
8分
即
 11分
11分
(用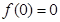 得
得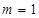 必须检验,不检验扣2分)
必须检验,不检验扣2分)
(3)由
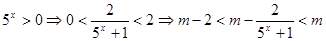
 14分
14分

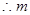 的取值范围是
的取值范围是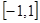 16分
16分
考点:1、函数单调性的证明;2、奇函数的定义;(3)函数的值域.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
 为奇函数.
为奇函数. 的值;
的值; 的图象由函数
的图象由函数 的图象先向右平移2个单位,再向上平移2个单位得到,写出
的图象先向右平移2个单位,再向上平移2个单位得到,写出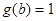 ,求
,求 的值.
的值. ,函数
,函数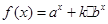
 且
且 ,
, 且
且 .
.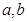 满足
满足 且
且 ,函数
,函数 是否具有奇偶性? 如果有,求出相应的
是否具有奇偶性? 如果有,求出相应的 值;如果没有,说明原因;
值;如果没有,说明原因; ,讨论函数
,讨论函数 .
. 时,判断
时,判断 的奇偶性,并说明理由;
的奇偶性,并说明理由; 时,若
时,若 ,求
,求 的值;
的值; ,且对任何
,且对任何 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的定义域为
的定义域为 ,
,  ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围. 。
。 的定义域;
的定义域; 的值,作出函数
的值,作出函数 的图象并指出函数
的图象并指出函数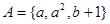 ,
,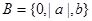 且
且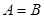 .
.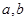 的值;
的值;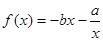 在
在 的单调性,并用定义加以证明.
的单调性,并用定义加以证明. ,当
,当 时,对应
时,对应 值的集合为
值的集合为 .
. 的值;(2)若
的值;(2)若 ,求该函数的最值.
,求该函数的最值.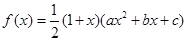 ,
,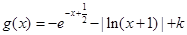
 的图像关于
的图像关于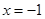 对称,且
对称,且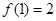 ,求
,求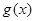 的图像的交点个数.
的图像的交点个数.