题目内容
设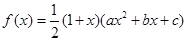 ,
,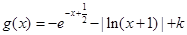
(1)若 的图像关于
的图像关于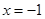 对称,且
对称,且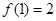 ,求
,求 的解析式;
的解析式;
(2)对于(1)中的 ,讨论
,讨论 与
与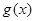 的图像的交点个数.
的图像的交点个数.
(1)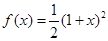 ;(2)见解析.
;(2)见解析.
解析试题分析:(1)因为函数图象关于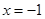 对称,故
对称,故 为二次函数且对称轴为
为二次函数且对称轴为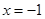 ∴
∴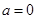
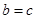 ,又
,又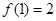 ,代入可求得函数解析式;(2)将问题转化为
,代入可求得函数解析式;(2)将问题转化为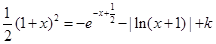 有几个解的问题,令
有几个解的问题,令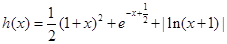 ,利用导数讨论其增减区间,当
,利用导数讨论其增减区间,当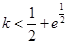 时,
时, 与
与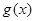 的图像无交点;当
的图像无交点;当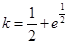 时,
时, 与
与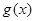 的图像有一个交点;当
的图像有一个交点;当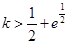 时,
时, 与
与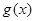 的图像有两个交点.
的图像有两个交点.
试题解析:(1)∵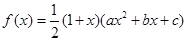 的图像关于
的图像关于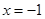 对称
对称
∴ 为二次函数且对称轴为
为二次函数且对称轴为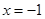 ∴
∴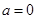
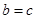
又∵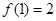 ∴
∴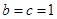 ∴
∴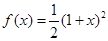
(2)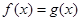 即
即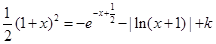
即 
令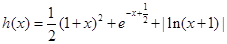
当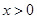 时
时 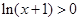
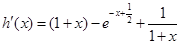
∵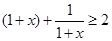
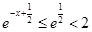 ∴
∴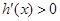
即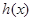 在
在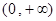 递增
递增
当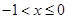 时
时 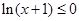
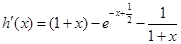
∵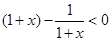
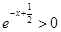 ∴
∴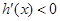
即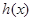 在
在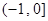 递减, ∵
递减, ∵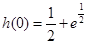
当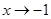 时
时 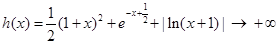
当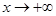 时
时 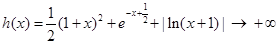
∴①当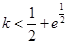 时,
时, 与
与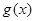 的图像无交点;
的图像无交点;
②当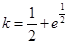 时,
时, 与
与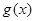 的图像有一个交点;
的图像有一个交点;
③当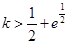 时,
时, 与
与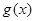 的图像有两个交点.
的图像有两个交点.
考点:利用导数研究函数的单调区间、函数与方程思想、函数解析式的求法.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目

 在
在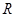 上单调递增;
上单调递增; 的值;
的值; ,求
,求 满足:当
满足:当 时,
时, ,当
,当 时,
时, .
. 表达式;
表达式; 与函数
与函数 的取值范围;
的取值范围;  满足什么条件时,直线
满足什么条件时,直线 的图像恰有
的图像恰有 个公共点
个公共点 ,且这
,且这 上.(不要求过程)
上.(不要求过程) .
. 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数; 与
与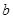 的值;
的值; 的解集.
的解集. 为奇函数.
为奇函数. ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明); ,使
,使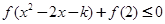 ,求实数k的最大值.
,求实数k的最大值. 为偶函数.
为偶函数.  的值;
的值; 有且只有一个根, 求实数
有且只有一个根, 求实数 的取值范围.
的取值范围.  是定义在
是定义在 上的减函数,满足
上的减函数,满足 .
. ;
; ,解不等式
,解不等式 .
. 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; 的单调性,并证明.
的单调性,并证明.
 若函数
若函数 在
在 和
和 上是增函数,在
上是增函数,在 是减函数,求
是减函数,求 的值;
的值; 讨论函数
讨论函数 的单调递减区间;
的单调递减区间; 如果存在
如果存在 ,使函数
,使函数 ,
,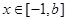
 ,在
,在 处取得最小值,试求
处取得最小值,试求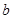 的最大值.
的最大值.