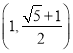题目内容
【题目】在三棱锥![]() 中,
中,![]() ,三角形
,三角形![]() 为等边三角形,二面角
为等边三角形,二面角![]() 的余弦值为
的余弦值为![]() ,当三棱锥
,当三棱锥![]() 的体积最大值为
的体积最大值为![]() 时,三棱锥
时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
【答案】![]()
【解析】
根据题意作出图象,利用三垂线定理找出二面角![]() 的平面角,再设出
的平面角,再设出![]() 的长,
的长,
即可求出三棱锥![]() 的高,然后利用利用基本不等式即可确定三棱锥
的高,然后利用利用基本不等式即可确定三棱锥![]() 的体积最大值,从而得出各棱的长度,最后根据球的几何性质,利用球心距,半径,底面半径之间的关系即可求出三棱锥
的体积最大值,从而得出各棱的长度,最后根据球的几何性质,利用球心距,半径,底面半径之间的关系即可求出三棱锥![]() 的外接球的表面积.
的外接球的表面积.
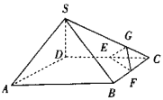
如图所示:
过点![]() 作
作![]() 面
面![]() ,垂足为
,垂足为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
则![]() 为二面角
为二面角![]() 的平面角的补角,即有
的平面角的补角,即有![]() .
.
∵易证![]() 面
面![]() ,∴
,∴![]() ,而三角形
,而三角形![]() 为等边三角形, ∴
为等边三角形, ∴![]() 为
为![]() 的中点.
的中点.
设![]() ,
, ![]() .
.
∴![]() .
.
故三棱锥![]() 的体积为
的体积为
![]()
当且仅当![]() 时,
时,![]() ,即
,即![]() .
.
∴![]() 三点共线.
三点共线.
设三棱锥![]() 的外接球的球心为
的外接球的球心为![]() ,半径为
,半径为![]() .
.
过点![]() 作
作![]() 于
于![]() ,∴四边形
,∴四边形![]() 为矩形.
为矩形.
则![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,解得
,解得![]() .
.
三棱锥![]() 的外接球的表面积为
的外接球的表面积为![]() .
.
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目