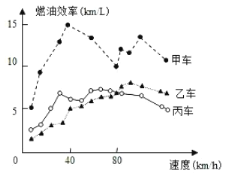
题目内容
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() .
.
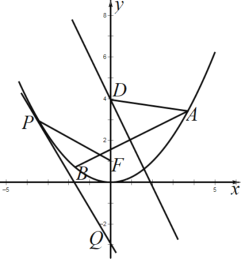
![]() 若点
若点![]() 为抛物线上异于原点的任一点,过点
为抛物线上异于原点的任一点,过点![]() 作抛物线的切线交
作抛物线的切线交![]() 轴于点
轴于点![]() ,证明:
,证明:![]() .
.
![]()
![]() ,
,![]() 是抛物线上两点,线段
是抛物线上两点,线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() (
(![]() 不与
不与![]() 轴平行),且
轴平行),且![]() .过
.过![]() 轴上一点
轴上一点![]() 作直线
作直线![]() 轴,且
轴,且![]() 被以
被以![]() 为直径的圆截得的弦长为定值,求
为直径的圆截得的弦长为定值,求![]() 面积的最大值.
面积的最大值.
【答案】![]() 证明见解析;
证明见解析; ![]()
![]() .
.
【解析】
![]() 设
设![]() 的坐标,求出在
的坐标,求出在![]() 处的导数,进而求出在
处的导数,进而求出在![]() 处的切线的方程,令
处的切线的方程,令![]() 求出
求出![]() 的坐标,进而求出
的坐标,进而求出![]() 的值,
的值,![]() 到准线的距离为
到准线的距离为![]() 的值可得
的值可得![]() ,进而可得结论;
,进而可得结论;
![]() 设直线
设直线![]() 的方程与抛物线联立求出两根之和及两根之积,进而求出弦长
的方程与抛物线联立求出两根之和及两根之积,进而求出弦长![]() ,再求线段
,再求线段![]() 的中点坐标,求出
的中点坐标,求出![]() 的中垂线的方程,将
的中垂线的方程,将![]() 点代入中垂线的方程可得参数的关系,设
点代入中垂线的方程可得参数的关系,设![]() 的坐标,由以
的坐标,由以![]() 为直径的圆截直线
为直径的圆截直线![]() 的弦长为定值可得
的弦长为定值可得![]() 的坐标,进而求出
的坐标,进而求出![]() 到直线
到直线![]() 的距离,代入面积公式可得关于直线
的距离,代入面积公式可得关于直线![]() 斜率的表达式,令函数求导可得函数的最大值,即求出面积的最大值.
斜率的表达式,令函数求导可得函数的最大值,即求出面积的最大值.
解:![]() 由抛物线的方程可得
由抛物线的方程可得![]() ,准线方程:
,准线方程:![]() ,设
,设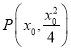 ,
,
由抛物线的方程可得![]() ,所以在
,所以在![]() 处的切线的斜率为:
处的切线的斜率为:![]() ,
,
所以在![]() 处的切线方程为:
处的切线方程为:![]() ,
,
令![]() ,可得
,可得![]() ,
,
即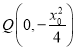 ,
,
所以![]() ,而
,而![]() 到准线的距离
到准线的距离![]() ,由抛物线的性质可得
,由抛物线的性质可得![]()
所以![]() ,
,![]() ,
,
可证得:![]() .
.
![]() 设直线
设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,
,![]() ,
,
直线与抛物线联立![]() ,
,
整理可得:![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
所以![]() 的中点坐标为:
的中点坐标为:![]() ,
,
所以线段![]() 的中垂线方程为:
的中垂线方程为:![]() ,
,
由题意中垂线过![]() ,所以
,所以![]() ,即
,即![]() ,①
,①
由抛物线的性质可得:![]() ,
,
所以![]() ,即
,即![]() ,②
,②
设![]() ,
,![]() ,
,
![]() 的中点的纵坐标为
的中点的纵坐标为![]() ,
,
所以以![]() 为直径的圆与直线
为直径的圆与直线![]() 的相交弦长的平方为:
的相交弦长的平方为:


![]() ,
,
要使以![]() 为直径的圆截得的弦长为定值则可得
为直径的圆截得的弦长为定值则可得![]() ,时相交弦长的平方为定值
,时相交弦长的平方为定值![]() ,即
,即![]()
所以![]() 到直线
到直线![]() 的距离为:
的距离为:![]() ,
,
而弦长![]()
![]() ,
,
所以![]() ,
,
将①代入可得![]()
![]() ,
,
设![]() 为偶函数,
为偶函数,
只看![]() 的情况即可,
的情况即可,
![]()
令![]() ,
,![]()
当![]() ,
,![]() ,
,![]() 单调递增;
单调递增;
当![]() ,
,![]() ,
,![]() 单调递减,
单调递减,
所以![]() 且
且![]() 上,
上, 为最大值
为最大值![]() ,
,
所以![]() 的最大值为:
的最大值为:![]() .
.

练习册系列答案
相关题目