题目内容
【题目】已知复数![]() 满足
满足![]() ,
,![]() 的虚部为2,
的虚部为2,
(1)求复数![]() ;
;
(2)设![]() 在复平面上对应点分别为
在复平面上对应点分别为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() 或
或![]() ;(2)1
;(2)1
【解析】
(1)设z=a+bi(a,b∈R),由已知列关于a,b的方程组,求解可得复数z;
(2)分类求得A、B、C的坐标,再由三角形面积公式求解.
解:(1)设z=a+bi(a,b∈R),
由已知可得: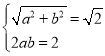 ,即
,即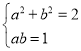 ,
,
解得![]() 或
或![]() .
.
∴z=1+i或z=﹣1﹣i;
(2)当z=1+i时,z2=2i,z﹣z2=1﹣i,
∴A(1,1),B(0,2),C(1,﹣1),
故△ABC的面积S![]() 2×1=1;
2×1=1;
当z=﹣1﹣i时,z2=2i,z﹣z2=﹣1﹣3i,
∴A(﹣1,﹣1),B(0,2),C(﹣1,﹣3),
故△ABC的面积S![]() 2×1=1.
2×1=1.
∴△ABC的面积为1.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目