题目内容
20．$C_n^0+C_n^1+…+C_n^r+…+C_n^n$=2n．分析 根据 ${C}_{n}^{0}$+${C}_{n}^{\;}$+${C}_{n}^{2}$+…+${C}_{n}^{n}$=（1+1）n，可得结论．
解答 解：${C}_{n}^{0}$+${C}_{n}^{\;}$+${C}_{n}^{2}$+…+${C}_{n}^{n}$=（1+1）n=2n，
故答案为：2n．
点评 本题主要考查二项式定理的应用，属于基础题．
练习册系列答案
相关题目
10．以抛物线y=$\frac{1}{4}$x2的焦点为圆心，且过坐标原点的圆的方程为（ ）
| A． | x2+y2-x=0 | B． | x2+y2-2x=0 | C． | x2+y2-y=0 | D． | x2+y2-2y=0 |
15．现有16张不同卡片，其中红色，黄色，蓝色，绿色卡片各4张，从中任取3张，要求这3张不能是同一颜色，且红色卡片至多1张，不同的取法为（ ）
| A． | 232种 | B． | 252种 | C． | 256种 | D． | 472种 |
5．
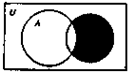已知集合A={x∈Z||x|≤1}，B={x|x2-2x=0}，若全集U=R，则图中的阴影部分表示的集合为（ ）
已知集合A={x∈Z||x|≤1}，B={x|x2-2x=0}，若全集U=R，则图中的阴影部分表示的集合为（ ）| A． | {-1} | B． | {2} | C． | {1，2} | D． | {0，2} |
9．a，b∈R，下列结论成立的是（ ）
| A． | 若a＜b，则ac＜bc | B． | 若a＜b，c＜d，则ac＜bd | ||
| C． | 若a＜b，则a-c＜b-c | D． | 若a＜b，则an＜bn（n∈N*，n≥2） |