题目内容
9.a,b∈R,下列结论成立的是( )| A. | 若a<b,则ac<bc | B. | 若a<b,c<d,则ac<bd | ||
| C. | 若a<b,则a-c<b-c | D. | 若a<b,则an<bn(n∈N*,n≥2) |
分析 A.取c≤0时,即可判断出正误;
B.举反例:取a=-2,b=-1,c=-4,d=-3,即可判断出正误;
C.利用不等式的基本性质即可判断出正误;
D.举反例:取a=-2,b=-1,则a2>b2,即可判断出正误.
解答 解:A.c≤0时不成立;
B.举反例:取a=-2,b=-1,c=-4,d=-3,则ab>cd,因此不成立;
C.∵a<b,∴a-c<b-c,正确;
D.举反例:取a=-2,b=-1,则a2>b2,因此不成立.
故选:C.
点评 本题考查了不等式的基本性质,考查了推理能力,属于基础题.

练习册系列答案
相关题目
19.给出命题:
(1)垂直于同一直线的两个平面平行;
(2)平行于同一直线的两个平面平行;
(3)平行于两相交平面的直线一定平行于这两相交平面的交线;
(4)平行于同一平面的两个平面平行;
其中正确命题个数有( )
(1)垂直于同一直线的两个平面平行;
(2)平行于同一直线的两个平面平行;
(3)平行于两相交平面的直线一定平行于这两相交平面的交线;
(4)平行于同一平面的两个平面平行;
其中正确命题个数有( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.已知$\overrightarrow{a}$=(-3,1),$\overrightarrow{b}$=(-1,2),若m$\overrightarrow{a}$-n$\overrightarrow{b}$=(10,0),(m,n∈R),则( )
| A. | m=2,n=4 | B. | m=3,n=-2 | C. | m=4,n=2 | D. | m=-4,n=-2 |
1.要从已编号(01~06)的60枚最新研制的某型导弹中随机抽取6枚来进行发射试验,用系统抽样方法确定所选取的6枚导弹的编号可能是( )
| A. | 5,15,25,36,45,55 | B. | 2,4,8,16,32,48 | ||
| C. | 2,12,23,34,45,56 | D. | 3,13,23,33,43,53 |
18.某人射击一次,命中8-10环及不足8环的概率如下表:
则此人命中环数超过8环(不含8环)的概率是0.28.
| 命中环数 | 不足8环 | 8环 | 9环 | 10环 |
| 概率 | 0•45 | 0•27 | x | 0•13 |
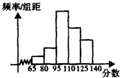 为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.
为了解某高三模拟考试学生数学学习情况,从该校参加质检的学生数学成绩中抽取一个样本,并分而5组,绘成如图所示的频率分布直方图,若第二组至第五组数据的频率分别为0.1,0.4,0.3,0.15,第一组数据的频数是2.