题目内容
设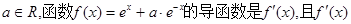
是奇函数，若曲线
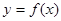的一条切线的斜率是
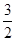，则切点的横坐标为 （ ）
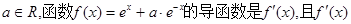是奇函数，若曲线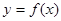的一条切线的斜率是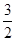，则切点的横坐标为 （ ）A． | B．— | C． | D． |
Ｄ
对函数求导，先有导函数为奇函数可求a，利用导数的几何意义设切点，表示切线的斜率，解方程可得．
解答：解：由题意可得，f ′(x)= ex-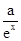
是奇函数
∴f′（0）=1-a=0
∴a=1，f（x）=ex+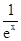
，f′(x)=ex-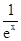
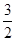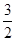曲线y=f（x）在（x，y）的一条切线的斜率是，即=ex-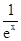
解方程可得ex=2?x=ln2
故选D
解答：解：由题意可得，f ′(x)= ex-
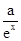是奇函数∴f′（0）=1-a=0
∴a=1，f（x）=ex+
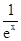，f′(x)=ex-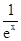曲线y=f（x）在（x，y）的一条切线的斜率是
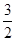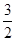，即=ex-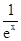解方程可得ex=2?x=ln2
故选D
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
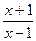（a＞0且a≠1）
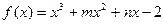的图像过点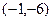
，且函数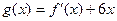
的图象的对称轴为
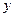轴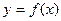
的解析式及它的单调递减区间
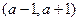内，求
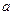的取值范围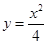
在点P（2, 1）处的切线方程为__________________________.
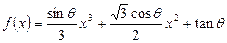，其中
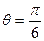，则导数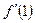
的值是( )
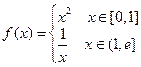（其中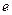
为自然对数的底数），则
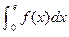的值为 
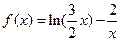的零点一定位于（ ）
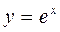在点P处的切线斜率为e，则点P的坐标为（ ）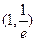 
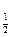（2x2-3x+1）的递减区间为 （ ）
）
］
，+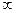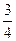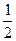