题目内容
已知函数f(x)=loga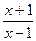 (a>0且a≠1)
(a>0且a≠1)
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)判断f(x)在(1,+∞)上的单调性,并予以证明.
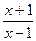 (a>0且a≠1)
(a>0且a≠1)(1)求f(x)的定义域;
(2)判断f(x)的奇偶性;
(3)判断f(x)在(1,+∞)上的单调性,并予以证明.
(1)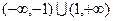 ;(2)奇函数;(3)略
;(2)奇函数;(3)略
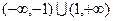 ;(2)奇函数;(3)略
;(2)奇函数;(3)略(1)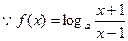
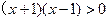
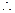 f(x)的定义域为
f(x)的定义域为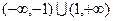 -----------------------(3分)
-----------------------(3分)
(2)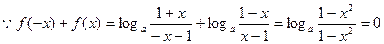
对定义域内的任意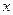 恒成立,所以函数为奇函数------
恒成立,所以函数为奇函数------ -----------------(3分)
-----------------(3分)
(3)法一:求导得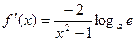 ,
,
①当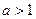 时,
时,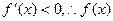 在
在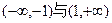 上都是减函数;
上都是减函数;
②当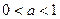 时,
时,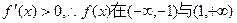 上都是增函数;
上都是增函数;
法二:设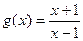 ,任取
,任取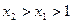 ,
,
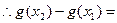
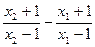
=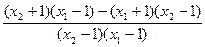 =
=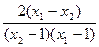 .-------------------(9分)
.-------------------(9分)
∵x1>1,x2>1,∴x1-1>0,x2-1>0.又∵x1<x2,∴x1-x2<0.
∴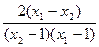 <0,即
<0,即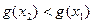 ,
,
当a> 1时,y=logax是增函数,∴loga
1时,y=logax是增函数,∴loga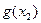 <loga
<loga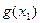 ,
,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,
∴loga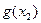 <loga
<loga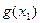 , 即f(x2)>f(x1).
, 即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga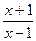 在(1,+∞)上为减函数;
在(1,+∞)上为减函数;
当0<a<1时,f(x)=loga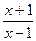 在(1,+∞)上为增函数.-----------------------(12分)
在(1,+∞)上为增函数.-----------------------(12分)
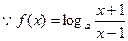
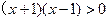
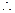 f(x)的定义域为
f(x)的定义域为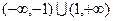 -----------------------(3分)
-----------------------(3分)(2)
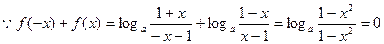
对定义域内的任意
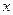 恒成立,所以函数为奇函数------
恒成立,所以函数为奇函数------ -----------------(3分)
-----------------(3分)(3)法一:求导得
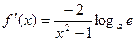 ,
,①当
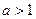 时,
时,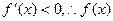 在
在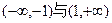 上都是减函数;
上都是减函数;②当
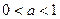 时,
时,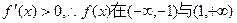 上都是增函数;
上都是增函数;法二:设
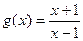 ,任取
,任取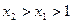 ,
,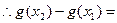
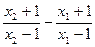
=
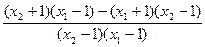 =
=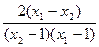 .-------------------(9分)
.-------------------(9分)∵x1>1,x2>1,∴x1-1>0,x2-1>0.又∵x1<x2,∴x1-x2<0.
∴
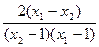 <0,即
<0,即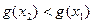 ,
,当a>
 1时,y=logax是增函数,∴loga
1时,y=logax是增函数,∴loga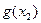 <loga
<loga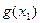 ,
, 即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,
∴loga
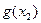 <loga
<loga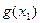 , 即f(x2)>f(x1).
, 即f(x2)>f(x1).综上可知,当a>1时,f(x)=loga
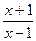 在(1,+∞)上为减函数;
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
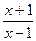 在(1,+∞)上为增函数.-----------------------(12分)
在(1,+∞)上为增函数.-----------------------(12分)
练习册系列答案
相关题目
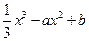 在x=-2处有极值.
在x=-2处有极值.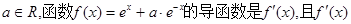 是奇函数,若曲线
是奇函数,若曲线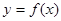 的一条切线的斜率是
的一条切线的斜率是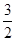 ,则切点的横坐标为 ( )
,则切点的横坐标为 ( )


 若对于任意
若对于任意 都有
都有 成立, 求实数
成立, 求实数 的取值范围.
的取值范围.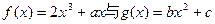 的图像都过点P(2,0),且在点P处
的图像都过点P(2,0),且在点P处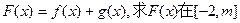 上的最小值。
上的最小值。

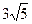
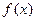 、
、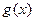 是定义域为R的恒大于零的可导函数,且
是定义域为R的恒大于零的可导函数,且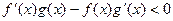 ,则当
,则当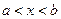 时有 ( )
时有 ( )



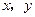 满足
满足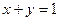 ,,则
,,则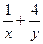 的最小值为______________
的最小值为______________