题目内容
函数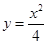
在点P（2, 1）处的切线方程为__________________________.
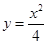在点P（2, 1）处的切线方程为__________________________.x-y-1=0
欲判在点P（2，1）处的切线方程，只须求出其斜率即可，故先利用导数求出在x=2处的导函数值，再结合导数的几何意义即可求出切线的斜率．从而问题解决．
解：∵函数y=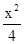
，
∴y′=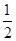
x，
∴在点P（2，1）处的切线的斜率为：
k=1，
∴在点P（2，1）处的切线方程为：
y-1=1×（x-2）
即：x-y-1=0．
故答案为：x-y-1=0．
解：∵函数y=
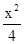，∴y′=
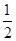x，∴在点P（2，1）处的切线的斜率为：
k=1，
∴在点P（2，1）处的切线方程为：
y-1=1×（x-2）
即：x-y-1=0．
故答案为：x-y-1=0．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
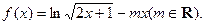
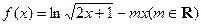的单调区间；
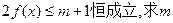的取值范围；
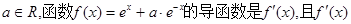是奇函数，若曲线
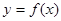的一条切线的斜率是
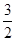，则切点的横坐标为 （ ）
在
上的单调性；
，使
，则称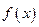
的不动点，现已知该函数有且仅有一个不动点，求
的值；
在
，
，
在
处取得最大值，求
的范围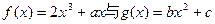
的图像都过点P（2，0），且在点P处
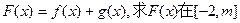上的最小值。
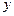与每日产量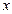
的函数关系式为
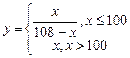，该工厂售出一件正品可获利
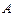元，但生产一件次品就损失
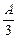元，为了获得最大利润，日产量应定为多少？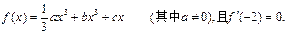
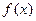在x=2处取得极小值－2，求
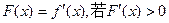的解集是A，且A∪（0，1）=（－∞，1），求
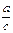的最大值.