题目内容
7.某驾校甲、乙、丙三名学员在考科目一前的10次模拟考试中通过的次数统计如表:| 学员 | 甲 | 乙 | 丙 |
| 通过的次数 | 9 | 8 | 9 |
(Ⅰ)求甲、乙、丙三名学员在正式考试中均未通过的概率
(Ⅱ)设甲、乙、丙三名学员在正式考试中通过的人数为ξ,求ξ的分布列及数学期望.
分析 (1)记甲、乙、丙三名学员考试通过分别为事件A,B,C,由题意得P(A)=0.9.P(B)=0.8,P(C)0.9.因为三个事件互相独立,继而求得概率
(2)随机变量可能取得值为0,1,2,3.得出各个值的概率,继而得到分布列期望值.
解答 解:(1)记甲、乙、丙三名学员考试通过分别为事件A,B,C,由题意得P(A)=0.9.P(B)=0.8,P(C)0.9.因为三个事件互相独立,则三名学员在正式考试中均为通过的概率P($\overrightarrow{A}\overrightarrow{B}\overrightarrow{C}$)=$P(\overline{A})P(\overline{B})P(\overline{C})$=0.1×0.2×0.1=0.002
(2)由题意得ξ的可能取值为0,1.2.3
P(ξ=0)=$P(\overline{A}\overline{B}\overline{C})$=0.002,P(ξ=1)=$P(\overline{A}\overline{B}C+\overline{B}\overline{C}A+\overline{A}B\overline{C})$=$P(\overline{A}\overline{B}C)+P(\overline{B}A\overline{C})+P(\overline{A}B\overline{C})$=0.1×0.2×0.9+0.9×0.9×0.1+0.1×0.8×0.1=0.044
P(ξ=2)=$P(\overline{A}BC+A\overline{B}C+AB\overline{C})$=$P(\overline{A}BC)+P(A\overline{B}C)+P(AB\overline{C})$=0.1×0.8×0.9+0.90.2×0.9+0.9×0.8×0.1=0.306
P(ξ=3)=P(ABC)=P(A)P(B)P(C)=0.9×0.8×0.9=0.648
故ξ的分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 0.002 | 0.044 | 0.306 | 0.648 |
点评 本题主要考查独立事件求概率和随机变量的分布列期望值,属于中档题型,在高考中经常考到,应引起重视.

| A. | f(x)=4x3+x | B. | f(x)=ln$\frac{5-x}{5+x}$ | C. | f(x)=sin$\frac{x}{2}$ | D. | f(x)=ex+e-x |
| A. | Φ | B. | [-2,2] | C. | [-1,1] | D. | {-1,1} |
| A. | 2 | B. | 3 | C. | 5 | D. | 6 |
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
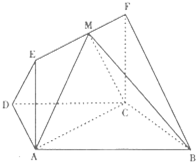 如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.