题目内容
已知函数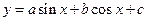
的图象上有一个最低点
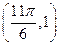，将图象上每个点的纵坐标不变，横坐标缩小到原来的
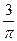，然后将所得图象向左平移一个单位得到
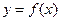的图象，若方程
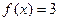的所有正根依次成为一个公差为3的等差数列，求 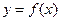的解析式.
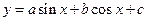的图象上有一个最低点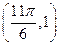，将图象上每个点的纵坐标不变，横坐标缩小到原来的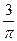，然后将所得图象向左平移一个单位得到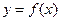的图象，若方程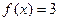的所有正根依次成为一个公差为3的等差数列，求 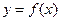的解析式. 
原函数可化为
（其中
为辅助角，满足
，
），
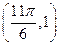是它的最低点，
解得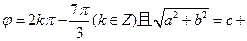
1,
按题给变换后得
方程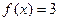的的正根就是直线
与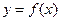的图象交点的横坐标，它们成等差数列，即与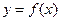相邻交点间的距离都相等.直线满足以上要求只能有三个位置：一是过图象最高点且和x轴平行的直线
，二是过图象最低点且和x轴平行的直线
，三是和、平行且等距的直线
，而图象最低点为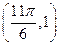，故不可能是．假若直线在
，交点间隔为一个周期６，即正根的公差为６，不合题意，所以只能在位置，所以
，，此时由
得
，正根可组成一个公差为3的等差数列，符合题意.
（其中为辅助角，满足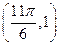，），是它的最低点， 解得
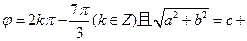1, 按题给变换后得方程
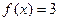的的正根就是直线与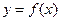的图象交点的横坐标，它们成等差数列，即与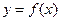相邻交点间的距离都相等.直线满足以上要求只能有三个位置：一是过图象最高点且和x轴平行的直线，二是过图象最低点且和x轴平行的直线，三是和、平行且等距的直线，而图象最低点为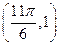，故不可能是．假若直线在，交点间隔为一个周期６，即正根的公差为６，不合题意，所以只能在位置，所以，，此时由得，正根可组成一个公差为3的等差数列，符合题意.
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
上为增函数且以
为周期的函数是
，且图像关于直线
对称的是（ ）
）|x|+
，有下面四个结论
，其中正确结论的个数为（ ）
； ④f（x）的最小值是－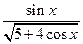
(0≤x≤2
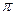)的值域是( )
]
]
]
]
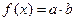，其中向量
，
，
.
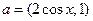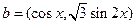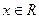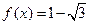，且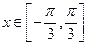
，求x的值；
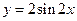的图像按向量
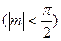平移后得到函数
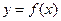的图像，求实数
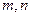的值。
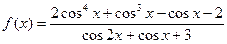
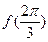的值 ②求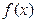
的周期 ③求
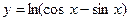的定义域是 .
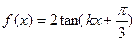的最小正周期
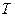满足
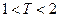,则自然数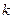
的值为______.