题目内容
关于函数f(x)=sin2x-( )|x|+
)|x|+ ,有下面四个结论
,有下面四个结论 ,其中正确结论的个数为( )
,其中正确结论的个数为( )
①f(x)是奇函数; ②当x>2009时,f(x)> 恒成立;
恒成立;
③f(x)的最大值是 ; ④f(x)的最小值是-
; ④f(x)的最小值是- ;
;
 )|x|+
)|x|+ ,有下面四个结论
,有下面四个结论 ,其中正确结论的个数为( )
,其中正确结论的个数为( )①f(x)是奇函数; ②当x>2009时,f(x)>
 恒成立;
恒成立;③f(x)的最大值是
 ; ④f(x)的最小值是-
; ④f(x)的最小值是- ;
;| A.1个 | B.2个 | C.3个 | D.4个 |
A
提示:显然f(x)为偶函数,结论①错;对于结论②,当x=1000π时,x>2009,sin21000π=0,∴f(1000π)= -(
-( )1000π<
)1000π< ,因此结论②错;
,因此结论②错;
又f(x)=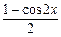 -(
-( )|x
)|x |+
|+ =1-
=1- cos2x-(
cos2x-( )|x|,-1≤cos2x≤1,
)|x|,-1≤cos2x≤1,
∴- ≤1-
≤1- cos2x≤
cos2x≤ ,故1-
,故1- cos2x-(
cos2x-( )|x|<
)|x|< ,即结论③错;而cos2x,(
,即结论③错;而cos2x,( )|x|在x=0时同时取得最大值,所以f(x)=1-
)|x|在x=0时同时取得最大值,所以f(x)=1- cos2x-(
cos2x-( )|x|在x=0时可取得最小值-
)|x|在x=0时可取得最小值- ,即结论④是正确的.
,即结论④是正确的.
 -(
-( )1000π<
)1000π< ,因此结论②错;
,因此结论②错;又f(x)=
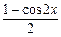 -(
-( )|x
)|x |+
|+ =1-
=1- cos2x-(
cos2x-( )|x|,-1≤cos2x≤1,
)|x|,-1≤cos2x≤1,∴-
 ≤1-
≤1- cos2x≤
cos2x≤ ,故1-
,故1- cos2x-(
cos2x-( )|x|<
)|x|< ,即结论③错;而cos2x,(
,即结论③错;而cos2x,( )|x|在x=0时同时取得最大值,所以f(x)=1-
)|x|在x=0时同时取得最大值,所以f(x)=1- cos2x-(
cos2x-( )|x|在x=0时可取得最小值-
)|x|在x=0时可取得最小值- ,即结论④是正确的.
,即结论④是正确的.
练习册系列答案
相关题目
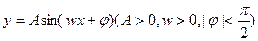 的图像上相邻的最高点与最低点的坐标分别为
的图像上相邻的最高点与最低点的坐标分别为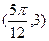 和
和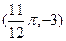 。 (1)求出
。 (1)求出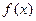 的解析式。(2)找出
的解析式。(2)找出 ,则
,则 ( )
( ) 上是增函数
上是增函数 上是减函数
上是减函数 上是增函数
上是增函数 上是减函数
上是减函数
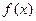 =
=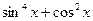 ,若
,若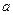 有解,求实数
有解,求实数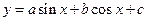 的图象上有一个最低点
的图象上有一个最低点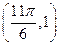 ,将图象上每个点的纵坐标不变,横坐标缩小到原来的
,将图象上每个点的纵坐标不变,横坐标缩小到原来的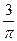 ,然后将所得图象向左平移一个单位得到
,然后将所得图象向左平移一个单位得到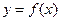 的图象,若方程
的图象,若方程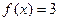 的所有正根依次成为一个公差为3的等差数列,求
的所有正根依次成为一个公差为3的等差数列,求  cosx+a=0在(0, 2π)内有相异二解α、β.
cosx+a=0在(0, 2π)内有相异二解α、β.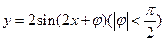 的图象经过点
的图象经过点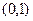 ,则该函数的一条对称轴方程为( ).
,则该函数的一条对称轴方程为( ). 




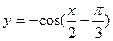 的单调递增区间是___________________________.
的单调递增区间是___________________________.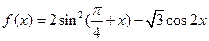 .若关于
.若关于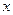 的方程
的方程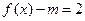 在
在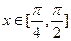 上有解,求实数
上有解,求实数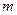 的取值范围.
的取值范围.