题目内容
已知数列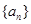 的首项
的首项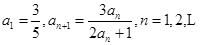 .
.
(1)求证: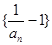 是等比数列,并求出
是等比数列,并求出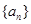 的通项公式;
的通项公式;
(2)证明:对任意的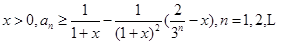 ;
;
(3)证明: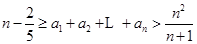 .
.
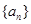 的首项
的首项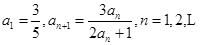 .
.(1)求证:
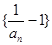 是等比数列,并求出
是等比数列,并求出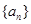 的通项公式;
的通项公式;(2)证明:对任意的
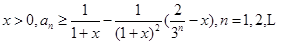 ;
;(3)证明:
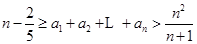 .
.(1)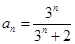 ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
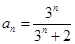 ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析试题分析:(1)将
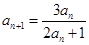 两边去倒数并常量分量,然后所得式子变形数列{
两边去倒数并常量分量,然后所得式子变形数列{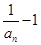 }的第n+1项是第n项若干倍形式,根据等比数列定义即可判定{
}的第n+1项是第n项若干倍形式,根据等比数列定义即可判定{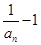 }是等比数列,利用等比数列通项公式,先求出{
}是等比数列,利用等比数列通项公式,先求出{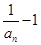 }的通项公式,再解出
}的通项公式,再解出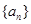 的通项公式;(2)将不等式右侧式子配凑
的通项公式;(2)将不等式右侧式子配凑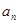 的通项公式形式,再将其化为关于
的通项公式形式,再将其化为关于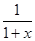 的二次函数最值问题,通过放缩即可证明该不等式;(3)先将
的二次函数最值问题,通过放缩即可证明该不等式;(3)先将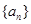 的通项公式常量分量,代入
的通项公式常量分量,代入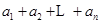 ,通过放缩即可证明不等式的左半部分,对
,通过放缩即可证明不等式的左半部分,对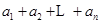 利用(2)的结论缩小,出现首项为
利用(2)的结论缩小,出现首项为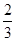 ,公比为
,公比为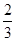 的等比数列的前n项和,数列取
的等比数列的前n项和,数列取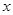 为该数列前n项和的算术平局值,即可证明该不等式右半部分.
为该数列前n项和的算术平局值,即可证明该不等式右半部分.试题解析:(1)
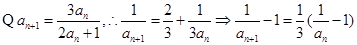 ,又
,又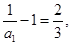
所以
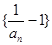 是以
是以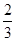 为首项,以
为首项,以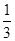 为公比的等比数列.
为公比的等比数列.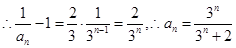 5分
5分(2)由(1)知
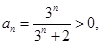
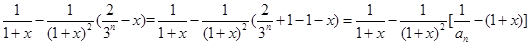
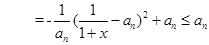 9分
9分 (3)先证左边不等式,由
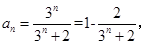 知
知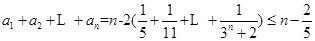 ;当
;当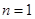 时等号成立; 11分
时等号成立; 11分再证右边不等式,由(2)知,对任意
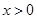 ,有
,有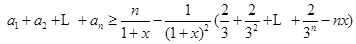 ,
,取
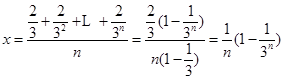 ,
,则
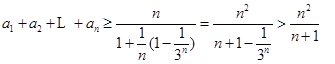 14分
14分考点:等比数列定义、通项公式、前n项和公式;二次函数最值;放缩法;转化与化归思想;运算求解能力

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
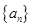 满足:
满足: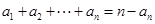 ,其中
,其中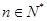 .
.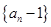 是等比数列;
是等比数列;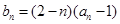 ,求数列
,求数列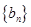 的最大项.
的最大项.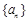 中,
中,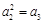 ,
,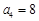 ,则
,则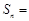 ___________.
___________. 中,
中, (c为非零常数)且前n项和
(c为非零常数)且前n项和 ,则实数k等于( ).
,则实数k等于( ). 1
1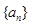 中,
中,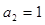 ,则其前
,则其前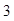 项的和
项的和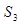 的取值范围是 ( )
的取值范围是 ( ) 



 中,
中, ,
, ,则
,则 的值 ( )
的值 ( )
