题目内容

已知：等差数列{an}中，a3+a4=15，a2a5=54，公差d＜0，求数列{an}的通项公式an．
∵{an}为等差数列，∴a2+a5=a3+a4，
∴
a2+a5=15
a2•a5=54
，
∵d＜0，则a5＜a2，解得
a2=9
a5=6
，
∴d=
a5-a2
5-2
=
6-9
3
=-1．
∴an=a2+（n-2）d=9-（n-2）=11-n．
练习册系列答案
相关题目
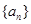已知数列的首项.
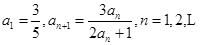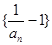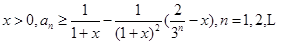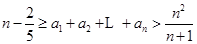（1）求证：是等比数列，并求出的通项公式；
（2）证明：对任意的；
（3）证明：.
等差数列{an}中，若Sp=Sr，则Sp+r的值为（　　）
A．pB．rC．0D．p+r
已知数列{an}的前n项和为Sn，且an=Sn•Sn-1(n≥2，Sn≠0)，a1=
2
9
．
（Ⅰ）求证：数列{
1
Sn
}为等差数列；
（Ⅱ）求满足an＜0的自然数n的集合．
设函数f（x）=
1
x-b
+1，若a，b，c成等差数列（公差不为零），则f（a）+f（c）=______．
在等差数列{an}中，a3+a4+a5=12，那么a2-a4+a6的值为（　　）
A．-4B．-2C．2D．4
在等差数列{an}中，a3=9，a9=3，则a12=（　　）
A．-3B．0C．3D．6
数列{an}中，an=3-2n，从第一项起各项依次为1，x，-3，y，…，那么x-y=（　　）
A．2B．-2C．4D．-4
等差数列{an}中a3=1，a6=7，则a9=（　　）
A．12B．13C．24D．25

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网