题目内容
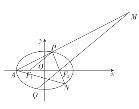
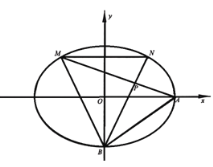
【题目】已知椭圆![]() 的短轴长为2,离心率为
的短轴长为2,离心率为![]() ,
,![]() ,
,![]() 分别是椭圆的右顶点和下顶点.
分别是椭圆的右顶点和下顶点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知![]() 是椭圆
是椭圆![]() 内一点,直线
内一点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,直线
,直线![]() 分别交椭圆于
分别交椭圆于![]() 两点,记
两点,记![]() ,
,![]() 的面积分别为
的面积分别为![]() ,
,![]() .
.
①若![]() 两点关于
两点关于![]() 轴对称,求直线
轴对称,求直线![]() 的斜率;
的斜率;
②证明:![]() .
.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②详见解析.
;②详见解析.
【解析】
(1)根据短轴长得![]() ,再根据离心率
,再根据离心率![]() 以及
以及![]() 的关系式可解得
的关系式可解得![]() ,从而可求得椭圆
,从而可求得椭圆![]() 的标准方程;
的标准方程;
(2)①设出![]() 的斜率
的斜率![]() ,写出
,写出![]() 的方程与椭圆联立解出
的方程与椭圆联立解出![]() 的坐标,再根据
的坐标,再根据![]() 的斜率关系得
的斜率关系得![]() 的斜率和方程与椭圆联立解出
的斜率和方程与椭圆联立解出![]() 的坐标,根据
的坐标,根据![]() ,
,![]() 关于
关于![]() 轴对称,列式可求得
轴对称,列式可求得![]() ;
;
②用![]() 的方程联立解得
的方程联立解得![]() 的坐标,通过两点间的距离算得
的坐标,通过两点间的距离算得![]() ,只要证明
,只要证明![]() ,就可证明
,就可证明![]() .
.
(1)椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() ,
,
所以![]() ,
,![]() ,
,
解得![]() .
.
所以椭圆方程为![]() .
.
(2)
①设直线![]() 的斜率为
的斜率为![]() ,则直线
,则直线![]() 的方程为
的方程为![]() ,
,
联立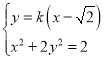 ,消去
,消去![]() 并化简得
并化简得![]() ,
,
解得![]() ,所以
,所以 .
.
因为直线![]() 的斜率乘积为
的斜率乘积为![]() ,所以直线
,所以直线![]() 的方程为
的方程为![]() ,
,
联立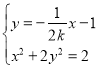 ,消去
,消去![]() 并化简得
并化简得![]() ,
,
解得![]() ,所以
,所以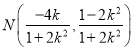 .
.
因为![]() 关于
关于![]() 轴对称,所以
轴对称,所以![]() ,
,
即![]() ,解得
,解得![]() .
.
当![]() 时,由
时,由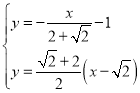 ,解得
,解得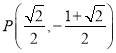 ,在椭圆
,在椭圆![]() 外,不满足题意.
外,不满足题意.
所以直线![]() 的斜率为
的斜率为![]() .
.
②由①得 ,
,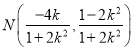 ,
,![]() ,
,
由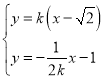 ,解得
,解得![]() .
.
即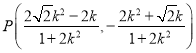 .
.
所以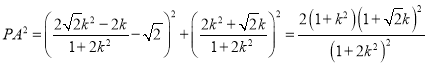 ,
,
 ,
,
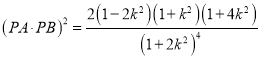 .
.
同理利用两点间的距离公式求得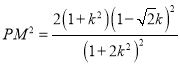 ,
,
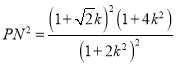 ,
,
所以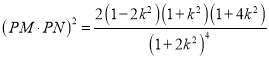 .
.
所以![]() ,
,
因为![]() ,所以
,所以
![]() .
.
即![]() .
.

【题目】某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
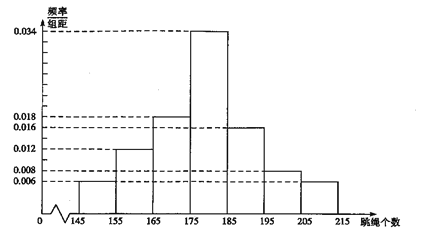
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.