题目内容
【题目】某学校高二年级举行了由全体学生参加的一分钟跳绳比赛,计分规则如下表:
每分钟跳绳个数 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
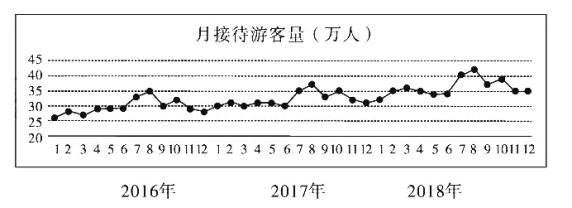
年级组为了解学生的体质,随机抽取了100名学生的跳绳个数作为一个样本,绘制了如下样本频率分布直方图.
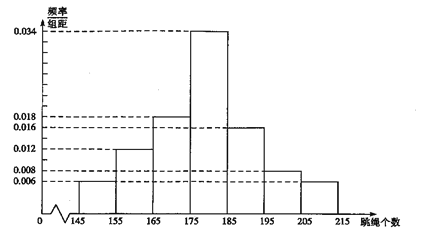
(1)现从样本的100名学生跳绳个数中,任意抽取2人的跳绳个数,求两人得分之和小于35分的概率;(用最简分数表示)
(2)若该校高二年级共有2000名学生,所有学生的一分钟跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() ,其中
,其中![]() ,
,![]() 为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
为样本平均数的估计值(同一组中数据以这组数据所在区间中点值作代表).利用所得的正态分布模型,解决以下问题:
(i)估计每分钟跳绳164个以上的人数(结果四舍五入到整数);
(ii)若在全年级所有学生中随机抽取3人,每分钟跳绳在179个以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望与方差.
的分布列和数学期望与方差.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【答案】(1)![]() ;(2)(i)1683;(ii)
;(2)(i)1683;(ii)![]() .
.
【解析】
(1)根据频率分布直方图得到16分,17分,18分的人数,再根据古典概率的计算公式求解.
(2)根据离散型随机变量的分布列和数学期望与方差的公式进行求解.
(1)设“两人得分之和小于35分”为事件![]() ,则事件
,则事件![]() 包括以下四种情况:
包括以下四种情况:
①两人得分均为16分;②两人中一人16分,一人17分;
③两人中一人16分,一人18分;④两人均17分.
由频率分布直方图可得,得16分的有6人,得17分的有12人,得18分的有18人,
则由古典概型的概率计算公式可得![]() .
.
所以两人得分之和小于35的概率为![]() .
.
(2)由频率分布直方图可得样本数据的平均数![]() 的估计值为:
的估计值为:
![]()
![]()
![]() (个).
(个).
又由![]() ,得标准差
,得标准差![]() ,
,
所以高二年级全体学生的跳绳个数![]() 近似服从正态分布
近似服从正态分布![]() .
.
(i)因为![]() ,所以
,所以![]() ,
,
故高二年级一分钟跳绳个数超过164个的人数估计为
![]() (人).
(人).
(ii)由正态分布可得,全年级任取一人,其每分钟跳绳个数在179以上的概率为![]() ,
,
所以![]() ,
,![]() 的所有可能的取值为0,1,2,3.
的所有可能的取值为0,1,2,3.
所以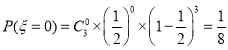 ,
,
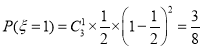 ,
,
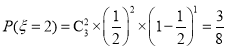 ,
,
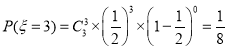 ,
,
故![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() ,
,![]() .
.

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案【题目】某企业为确定下一年度投入某种产品的生产所需的资金,需了解每投入2千万资金后,工人人数![]() (单位:百人)对年产能
(单位:百人)对年产能![]() (单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
(单位:千万元)的影响,对投入的人力和年产能的数据作了初步处理,得到散点图和统计量表.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
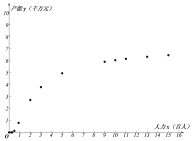
(1)根据散点图判断:![]() 与
与![]() 哪一个适宜作为年产能
哪一个适宜作为年产能![]() 关于投入的人力
关于投入的人力![]() 的回归方程类型?并说明理由?
的回归方程类型?并说明理由?
(2)根据(1)的判断结果及相关的计算数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)现该企业共有2000名生产工人,资金非常充足,为了使得年产能达到最大值,则下一年度共需投入多少资金(单位:千万元)?
附注:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为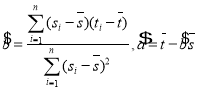 ,(说明:
,(说明:![]() 的导函数为
的导函数为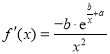 )
)
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):

若分数不低于95分,则称该员工的成绩为“优秀”.
(1)从这20人中任取3人,求恰有1人成绩“优秀”的概率;
(2)根据这20人的分数补全下方的频率分布表和频率分布直方图,并根据频率分布直方图解决下面的问题.
组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
①估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表);
②若从所有员工中任选3人,记![]() 表示抽到的员工成绩为“优秀”的人数,求
表示抽到的员工成绩为“优秀”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.