题目内容
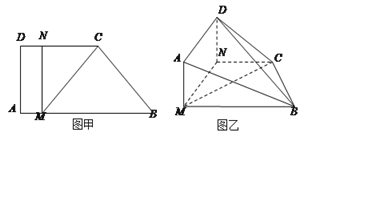
【题目】如图甲,直角梯形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在
分别在![]() 上,且
上,且![]() ,
, ![]() ,
, ![]() ,现将梯形
,现将梯形![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 与平面
与平面![]() 垂直(如图乙).
垂直(如图乙).
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(II)当![]() 的长为何值时,二面角
的长为何值时,二面角![]() 的大小为
的大小为![]() ?
?
【答案】(Ⅰ)见解析;(Ⅱ) ![]() .
.
【解析】试题分析:
(1)建立空间直角坐标系,结合直线的方向向量和平面的一个法向量即可证得线面平行;
(2)结合空间直角坐标系探究可得![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.
试题解析:
(Ⅰ)如图建立空间直角坐标系N-xyz.
设![]() ,则A(2,0,t),B(2,4,0),
,则A(2,0,t),B(2,4,0), ![]()
又易知平面DNC的一个法向量为![]() ,
,
由![]() ,得AB∥平面DNC.
,得AB∥平面DNC.
(Ⅱ)设![]() ,则D(0,0,t),C(0,2,0),B(2,4,0),故
,则D(0,0,t),C(0,2,0),B(2,4,0),故![]() (0,-2,t),
(0,-2,t), ![]() (2,2,0),
(2,2,0),
设平面DBC的一个法向量为![]() ,则
,则![]()
取![]() ,则
,则![]() ,即
,即![]() ,
,
又易知平面BCN的一个法向量为![]() ,
,
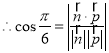 ,即
,即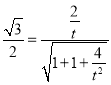 ,解得
,解得![]() .
.
另解:(Ⅰ)∵MB∥NC,MB![]() 平面DNC,NC
平面DNC,NC![]() 平面DNC,
平面DNC,
∴MB∥平面DNC. 同理MA∥平面DNC,
又MA∩MB=M且MA、MB![]() 平面MAB,
平面MAB,
∴平面MAB∥平面NCD, 又AB![]() 平面MAB,
平面MAB,
∴AB∥平面NCD.
(Ⅱ)过N作NH⊥BC交BC延长线于H,连结DH,
∵平面AMND⊥平面MNCB,DN⊥MN
∴DN⊥平面MNCB,从而DH⊥BC,
∴∠DHN为二面角D-BC-N的平面角.
由已知得, ![]() ,∴
,∴![]() ,
, ![]() ,
,
∴![]() .
.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目