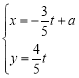题目内容
【题目】下列说法正确的是( )
A. “
为真”是“
为真”的充分不必要条件；
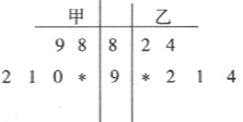
B. 样本
的标准差是3.3；
C. K2是用来判断两个分类变量是否相关的随机变量，当K2的值很小时可以推定两类变量不相关；
D. 设有一个回归直线方程为
，则变量
每增加一个单位，
平均减少1.5个单位.
【答案】D
【解析】逐一分析所给的选项：
A，p∧q为真，则p、q均为真，p∨q为真，p、q至少一个为真，故“p∨q为真”是“p∧q为真”的必要不充分条件，故不正确；
B,样本10,6,8,5,6的平均数为7,方差为
,标准差是
，故不正确；
C,K2的值很小时，只能说两个变量的相关程度低，不能推定两个变量不相关。所以C错；
D,设有一个回归直线方程为
，则变量x毎增加一个单位，y平均减少1.5个单位，正确。
本题选择D选项.
练习册系列答案
相关题目
【题目】某城市一汽车出租公司为了调查A，B两种车型的出租情况，现随机抽取了这两种车型各100辆，分别统计了每辆车某个星期内的出租天数，统计数据如下表：
A车型 B车型
出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 | 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
（Ⅰ）从出租天数为3天的汽车（仅限A，B两种车型）中随机抽取一辆，估计这辆汽车恰好是A型车的概率；
（Ⅱ）根据这个星期的统计数据，估计该公司一辆A型车，一辆B型车一周内合计出租天数恰好为4天的概率；
（Ⅲ）
（ⅰ）试写出A，B两种车型的出租天数的分布列及数学期望；
（ⅱ）如果两种车辆每辆车每天出租获得的利润相同，该公司需要从A，B两种车型中购买一辆（注：两种车型的采购价格相当），请你根据所学的统计知识，建议应该购买哪一种车型，并说明你的理由．
