题目内容
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
试题分析:(1)记事件![]() {从甲箱中摸出的1个球是红球},
{从甲箱中摸出的1个球是红球},![]() {从乙箱中摸出的1个球是红球}
{从乙箱中摸出的1个球是红球}
![]() {顾客抽奖1次获一等奖},
{顾客抽奖1次获一等奖},![]() {顾客抽奖1次获二等奖},
{顾客抽奖1次获二等奖},![]() {顾客抽奖1次能获奖},则可知
{顾客抽奖1次能获奖},则可知![]()
与![]() 相互独立,
相互独立,![]() 与
与![]() 互斥,
互斥,![]() 与
与![]() 互斥,且
互斥,且![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,再
,再
利用概率的加法公式即可求解;(2)分析题意可知![]() ,分别求得
,分别求得![]() ,
,![]() ,
,![]() ,
,![]() ,即可知
,即可知![]() 的概率分布及其期望.
的概率分布及其期望.
试题解析:(1)记事件![]() {从甲箱中摸出的1个球是红球},
{从甲箱中摸出的1个球是红球},![]() {从乙箱中摸出的1个球是红球}
{从乙箱中摸出的1个球是红球}
![]() {顾客抽奖1次获一等奖},
{顾客抽奖1次获一等奖},![]() {顾客抽奖1次获二等奖},
{顾客抽奖1次获二等奖},![]() {顾客抽奖1次能获奖},由题意,
{顾客抽奖1次能获奖},由题意,![]() 与
与![]() 相互独立,
相互独立,![]() 与
与![]() 互斥,
互斥,![]() 与
与![]() 互斥,且
互斥,且![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
![]()
![]() ,故所求概率为
,故所求概率为![]() ;(2)顾客抽奖3次独立重复试验,由(1)知,顾客抽奖1次获一等奖的概率为
;(2)顾客抽奖3次独立重复试验,由(1)知,顾客抽奖1次获一等奖的概率为![]() ,∴
,∴![]() ,
,
于是![]() ,
,![]() ,
,![]() ,
,
![]() ,故
,故![]() 的分布列为
的分布列为
| 0 | 1 | 3 | |
|
|
|
|
|
![]() 的数学期望为
的数学期望为 ![]() .
.

练习册系列答案
相关题目
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
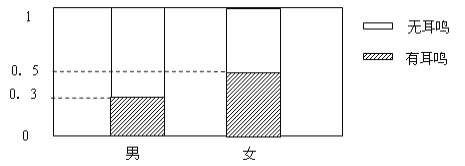
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()