题目内容
【题目】设函数![]() ,
,![]() .
.
(1)当![]() (
(![]() 为自然对数的底数)时,求
为自然对数的底数)时,求![]() 的最小值;
的最小值;
(2)讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)![]() 的最小值是
的最小值是![]() ;(2)当
;(2)当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点;当
有且只有一个零点;当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.
【解析】
试题分析:(1)求函数的导数![]() ,函数的极值点为
,函数的极值点为![]() ,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据
,所以得到函数的单调区间,也就得到函数的最小值了;(2)根据![]() ,参变分离后得到
,参变分离后得到![]() ,设
,设![]() ,通过导数求函数的单调性,以及图象特征,转化为
,通过导数求函数的单调性,以及图象特征,转化为![]() 与函数的交点个数问题.
与函数的交点个数问题.
试题解析:(1)当![]() 时,
时,![]() ,∴
,∴![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函;
上是增函;
∴当![]() 时,
时,![]() 取最小值
取最小值![]() .
.
(2)∵函数![]() ,
,
令![]() ,得
,得![]() ;
;
设![]() ,则
,则![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是增函数;
上是增函数;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上是减函数;
上是减函数;
当![]() 是
是![]() 的极值点,且是唯一极大值点,∴
的极值点,且是唯一极大值点,∴![]() 是
是![]() 的最大值点;
的最大值点;
∴![]() 的最大值为
的最大值为![]() ,又
,又![]() 结合
结合![]() 的图像,
的图像,
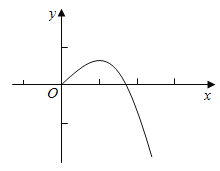
可知:
①当![]() 时,函数
时,函数![]() 无零点;
无零点;
②当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
③当![]() 时,函数
时,函数![]() 有两个零点;
有两个零点;
④当![]() 时,函数
时,函数![]() 有且只有一个零点;
有且只有一个零点;
综上:
当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有且只有一个零点;当
有且只有一个零点;当![]() 时,函数
时,函数![]() 有且只有两个零点.
有且只有两个零点.

练习册系列答案
相关题目
【题目】随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
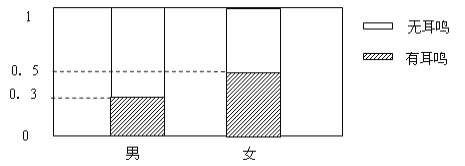
绘出2×2列联表;
②根据列联表的独立性检验,能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系?
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附:![]()
![]()