题目内容
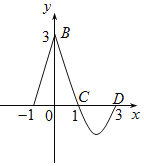
【题目】抛物线C:y2=2px(p>0)的准线为l,焦点为F.⊙M的圆心在x轴的正半轴上,且与y轴相切.过原点O作倾斜角为![]() 的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
的直线n交l于点A, 交⊙M于另一点B,且AO=OB=2.
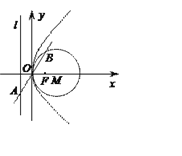
(1)求⊙M和抛物线C的方程;
(2)若P为抛物线C上的动点,求![]() 的最小值;
的最小值;
(3)过l上的动点Q向⊙M作切线,切点为S,T,求证:直线ST恒过一个定点,并求该定点的坐标.
【答案】(1)(x-2)2+y2=4。 (2)2.(3)![]() .
.
【解析】试题分析:(1)根据![]() 可求出
可求出![]() 的值,从而求出抛物线方程,求出圆心和半径可求出
的值,从而求出抛物线方程,求出圆心和半径可求出![]() 的方程;(2)先表示出
的方程;(2)先表示出![]() 然后根据点在抛物线上将
然后根据点在抛物线上将![]() 消去,求关于
消去,求关于![]() 的二次函数的最小值即可;(3)以点
的二次函数的最小值即可;(3)以点![]() 这圆心,
这圆心,![]() 为半径作
为半径作![]() ,则线段
,则线段![]() 即为
即为![]() 与
与![]() 的公共弦,设点
的公共弦,设点![]() ,根据
,根据![]() ,求出直线
,求出直线![]() 的方程,使直线与
的方程,使直线与![]() 无关,可求出定点坐标.
无关,可求出定点坐标.
试题解析:(1)因为=OA·cos60°=2×=1,即p=2,所以抛物线C的方程为y2=4x
设⊙M的半径为r,则r=![]() ·
·![]() =2,所以⊙M的方程为(x-2)2+y2=4。
=2,所以⊙M的方程为(x-2)2+y2=4。
(2)设P(x,y)(x≥0),则![]() ·
·![]() =(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
=(2-x,-y)(1-x,-y)=x2-3x+2+y2=x2+x+2,
所以当x=0时,![]() ·
·![]() 有最小值为2.
有最小值为2.
(3)以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦.
设点Q(-1,t),则QS2=QM2-4=t2+5,所以⊙Q的方程为(x+1)2+(y-t)2=t2+5,
从而直线QS的方程为3x-ty-2=0(*),
因为![]() 一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).
一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为(,0).

练习册系列答案
相关题目