题目内容
【题目】已知抛物线C的一个焦点为
，对应于这个焦点的准线方程为
（1）写出抛物线C的方程；
（2）过F点的直线与曲线C交于A、B两点，O点为坐标原点，求△AOB重心G的轨迹方程；
（3）点P是抛物线C上的动点，过点P作圆
的切线，切点分别是M，N.当P点在何处时，|MN|的值最小？求出|MN|的最小值.
【答案】（1）抛物线方程为： 
；（2）
；（3）P（2，±2），|MN|取最小值
.
【解析】试题分析：
(1)由直线方程可得抛物线方程为
；
(2)利用重心坐标公式消去参数可得轨迹方程为： 
；
(3)利用圆的性质结合题意可得满足题意时点P的坐标为P（2，±2），且|MN|取最小值
.
试题解析：
（1）抛物线方程为： 
.
（2）①当直线不垂直于x轴时，设方程为
，代入
，
得： 
设
，则
， 
设△AOB的重心为
则
，
消去k得
为所求，
②当直线垂直于x轴时， 
△AOB的重心
也满足上述方程.
综合①②得，所求的轨迹方程为
（3）设已知圆的圆心为Q（3，0），半径
，
根据圆的性质有：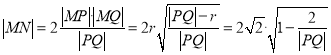 
当|PQ|2最小时，|MN|取最小值，
设P点坐标为
，则
∴当
， 
时， 
取最小值5，
故当P点坐标为（2，±2）时，|MN|取最小值
.
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
