Question

14．已知菱形ABCD的对角线AC长为1，则$\overrightarrow{AD}•\overrightarrow{AC}$=$\frac{1}{2}$．

Answer 1

分析 画出菱形ABCD，由对角线互相垂直，结合数量积的几何意义，计算即可得到所求值．

解答 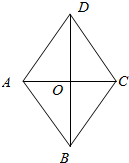解：如图菱形ABCD，连接AC，BD交于O点，
则AC⊥BD，
即有$\overrightarrow{AD}•\overrightarrow{AC}$=|$\overrightarrow{AD}$|•|$\overrightarrow{AC}$|•cos∠DAC
=$\frac{1}{2}$|$\overrightarrow{AO}$|•|$\overrightarrow{AC}$|=$\frac{1}{2}$×1=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．

点评 本题考查向量的数量积的求法，注意运用定义和投影的意义，考查运算能力，属于基础题．