题目内容
14.已知函数y=mx2-2x+1.(1)如果m=1,且x∈[-2,1],求函数y的取值范围;
(2)解关于m的方程f(m)=0;
(3)当x∈[1,2]时,y≥0恒成立,求实数m的范围.
分析 (1)求出对称轴,判断区间[-2,1]为减区间,即可得到最值,进而得到所求范围;
(2)运用因式分解的方法,即可得到方程的解;
(3)运用参数分离,再由配方求得右边的最值,进而得到m的范围.
解答 解:(1)m=1时,y=x2-2x+1=(x-1)2,
区间[-2,1]在对称轴x=1的左边,为减区间,
即有最小值为(1-1)2=0,最大值为(-2-1)2=9,
则y的取值范围是[0,9];
(2)f(m)=m•m2-2m+1=0,
即有(m-1)(m2+m-1)=0,
解得m=1或m=$\frac{-1±\sqrt{5}}{2}$;
(3)当x∈[1,2]时,y≥0恒成立,
即为m≥$\frac{2}{x}$-$\frac{1}{{x}^{2}}$的最大值,
由g(x)=$\frac{2}{x}$-$\frac{1}{{x}^{2}}$=-($\frac{1}{x}$-1)2+1,
$\frac{1}{x}$∈[$\frac{1}{2}$,1],为递增区间,
即有g(1)取得最大值,且为1,
则m≥1.
即有实数m的范围是[1,+∞).
点评 本题主要考查二次函数的值域和最值的求法,注意对称轴和区间的关系,考查运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.在一个不透明的口袋里装有外观相同的白球和黑球共20个,某学习小组做摸球试验,试验方法如图所示,试验得到了一组统计数据(表1)
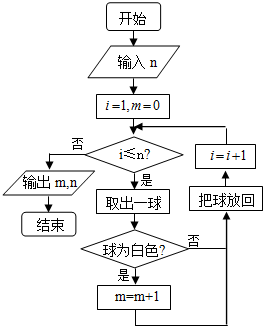
①请估计:当n很大时,摸到白球的频率将会接近0.60.
②假如你去摸一次球,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
③口袋中白球的个数约为12,黑球的个数约为8.
表1:

①请估计:当n很大时,摸到白球的频率将会接近0.60.
②假如你去摸一次球,你摸到白球的概率是0.6,摸到黑球的概率是0.4;
③口袋中白球的个数约为12,黑球的个数约为8.
表1:
| n | 100 | 150 | 200 | 500 | 800 | 1000 |
| m | 58 | 96 | 116 | 295 | 484 | 601 |
2.函数f(x)=ex+e-x,g(x)=f(2x)+mf(x),对任意x∈R,g(x)≥0,则m的取值范围是( )
| A. | [-4,+∞) | B. | [-1,+∞) | C. | [0,+∞) | D. | [2,+∞) |
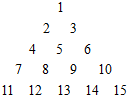 把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
 如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.
如图,有-直角墙角,两边的长度足够长,在P处有-棵树与两墙的距离分别是a米(0<a<12),4米,不考虑树的粗细,现在想用16米长的篱笆,借助墙角围成-个矩形的花围ABCD,并要求将这棵树围在花圃内或在花圃的边界上.设BC=x米,此矩形花围的面积为y平方米.