题目内容
9.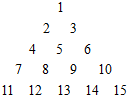 把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
分析 根据题意,可以归纳出:第n行有n个数(n≥3),且每行从左到右为公差为1的等差数列,可得前n行共有1+2+3+4+…+n=$\frac{1}{2}$ n(n+1)个数,进而可得答案
解答 解:根据题意,分析所给的数阵可得,第n行有n个数(n≥3),且每行从左到右为公差为1的等差数列,
则前n行共有1+2+3+4+…+n=$\frac{1}{2}$ n(n+1)个数,
则前n-1行共有1+2+3+4+…+(n-1)=$\frac{1}{2}$ n(n-1)个数,
则第n行从左向右的第1个数是$\frac{1}{2}$ n(n-1)+1,
则第n行从左向右的第3个数是$\frac{1}{2}$ n(n-1)+3=$\frac{{n}^{2}-n+6}{2}$,(n≥3)
点评 本题考查归纳推理的运用,关键在于发现数阵中各行数的变化规律

练习册系列答案
相关题目
19.在△ABC中,若sinAcosB=1-cosAsinB,则△ABC为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法判定 |
1.某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为
(Ⅰ)求该生至少有1门课程取得优秀成绩的概率及求p,q的值;
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.