Question

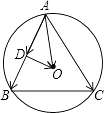
【题目】在△ABC中，内角A，B，C的对边分别为a，b，c，已知2acosB=2c﹣b，若O是△ABC外接圆的圆心，且 ，则m= ．

Answer 1

【答案】
【解析】解：△ABC中，2acosB=2c﹣b， ∴2a =2c﹣b，
∴b2+c2﹣a2=bc，
∴cosA= = = ；
又A∈（0，π），∴A= ；
由O是△ABC外接圆的圆心，取AB中点D，
则有 = + ，如图所示；
∴ + =m =m（ + ）；
由 ⊥ 得 =0，
∴ + =m（ + ）
=m +m = m ，
即 c2+ bccosA= mc2；
由正弦定理化简得 sin2C+ sinBsinCcosA= msin2C，
由sinC≠0，两边同时除以sinC得：cosB+cosAcosC= msinC，
∴ m=
=
=
=sinA=sin = ，
解得m= ．
所以答案是： ．