题目内容
18.已知△ABC的顶点坐标分别为A(1,1),B(m,1),C(4,5),(1)若m=5,求cos2A;
(2)若∠ABC为直角,求实数m的取值.
分析 (1)若m=5,求出三角形的边长,利用余弦定理求出cosA,即可求cos2A;
(2)若∠ABC为直角,$\overrightarrow{AB}$$•\overrightarrow{BC}$=0,建立方程关系即可得到结论.
解答 解:(1)若m=5,则B(5,1),
则|AB|=5-1=4,|AC|=$\sqrt{{3}^{2}+{4}^{2}}=5$,|BC|=$\sqrt{1+{4}^{2}}$=$\sqrt{17}$,
则cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{{4}^{2}+{5}^{2}-17}{2×4×5}$=$\frac{3}{5}$,
则cos2A=2cos2A-1=2×($\frac{3}{5}$)2-1=-$\frac{7}{25}$;
(2)若∠ABC为直角,则$\overrightarrow{AB}$$•\overrightarrow{BC}$=0,
即(m-1,0)•(4-m,4)=0,
即(m-1)•(4-m)=0,
解得m=1(舍)或m=4.
点评 本题主要考查解三角形的应用,利用余弦定理求出cosA,以及三角函数的倍角公式是解决本题的关键.

练习册系列答案
相关题目
12.使cosx=1-m有意义的m的取值范围为( )
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |
10.函数f(x)=-3x在区间[1,2]上的最小值是( )
| A. | -9 | B. | -6 | C. | -3 | D. | -$\frac{1}{3}$ |
7.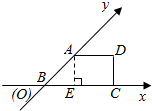 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
 有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )
有一块多边形的菜地它的水平放置的平面图形的斜二测直观图是直角梯形,如图所示∠ABC=45°AB=2,AD=1,DC⊥BC,则这块菜地的面积为.( )| A. | 2+2$\sqrt{2}$ | B. | 4+2$\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 1+$\sqrt{2}$ |
8.在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人.女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断性别与休闲方式是否有关系?
本题参考:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+c)(b+d)(a+b)(c+d)}$.
(Ⅰ)根据以上数据建立一个2×2的列联表;
(Ⅱ)判断性别与休闲方式是否有关系?
| P(k2>k) | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 3.84 | 5.024 | 6.635 | 7.879 |