题目内容
14.(1)已知$α,β∈(\frac{3π}{4},π),sin(α+β)=-\frac{3}{5},sin(β-\frac{π}{4})=\frac{12}{13}$,求$cos(α+\frac{π}{4})$的值.(2)求$sin{50}^{?}(1+\sqrt{3}tan{10}^{?})$的值.
分析 (1)由条件利用同角三角函数的基本关系求得cos(α+β)和cos(β-$\frac{π}{4}$)的值,再利用两角和差的三角公式求得$cos(α+\frac{π}{4})$=cos[(α+β)-(β-$\frac{π}{4}$)]的值.
(2)由条件利用同角三角函数的基本关系,二倍角公式、诱导公式求得所给式子的值.
解答 解:(1)∵已知$α,β∈(\frac{3π}{4},π),sin(α+β)=-\frac{3}{5},sin(β-\frac{π}{4})=\frac{12}{13}$,∴α+β∈($\frac{3π}{2}$,2π),β-$\frac{π}{4}$∈($\frac{π}{2}$,$\frac{3π}{4}$),
∴cos(α+β)=$\sqrt{{1-sin}^{2}(α+β)}$=$\frac{4}{5}$,cos(β-$\frac{π}{4}$)=-$\sqrt{{1-sin}^{2}(β-\frac{π}{4})}$=-$\frac{5}{13}$.
$cos(α+\frac{π}{4})$=cos[(α+β)-(β-$\frac{π}{4}$)]=cos(α+β)cos(β-$\frac{π}{4}$)+sin(α+β)sin(β-$\frac{π}{4}$)=$\frac{4}{5}×(-\frac{5}{13})$+(-$\frac{3}{5}$)•$\frac{12}{13}$=-$\frac{56}{65}$.
(2)$sin{50}^{?}(1+\sqrt{3}tan{10}^{?})$=sin50°•$\frac{cos10°+\sqrt{3}sin10°}{cos10°}$=sin50°•$\frac{2sin(10°+30°)}{cos10°}$=cos40°•$\frac{2sin40°}{cos10°}$=$\frac{sin80°}{cos10°}$=1.
点评 本题主要考查同角三角函数的基本关系,二倍角公式,两角和差的三角公式,以及三角函数在各个象限中的符号,属于基础题.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{-1+\sqrt{2}}{2}$ | C. | -1 | D. | $\frac{1-\sqrt{2}}{2}$ |
| A. | 若sinA+cosA<1,则△ABC为钝角三角形 | |
| B. | 若a2+b2<c2,则△ABC为钝角三角形 | |
| C. | 若$\overrightarrow{AB}$•$\overrightarrow{BC}$<0,则△ABC为钝角三角形 | |
| D. | 若A、B为锐角且cosA>sinB,则△ABC为钝角三角形 |
?①y=sinx的递增区间是[2k$π,2kπ+\frac{π}{2}$]
?②y=sinx是递增函数.
?③y=sinx在$[{-\frac{π}{2},\frac{π}{2}}]$上是增函数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 0个 |
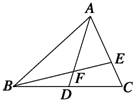
| A. | 4:1 | B. | 3:1 | C. | 2:1 | D. | 5:1 |
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |