��Ŀ����
����Ŀ��ij���г���Ϊ����������˾��������ʽ�ĵ�������֪��������ʽ�����Ĺ̶��ɱ�Ϊ20000Ԫ��ÿ����һ������ʽ������Ҫ����Ͷ��100Ԫ�����ݳ������㣬���г����������棨��λ��Ԫ������ֶκ���h��x��������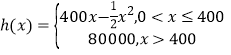 ,x������ʽ�������²�������λ������������=�����橁�ܳɱ���
,x������ʽ�������²�������λ������������=�����橁�ܳɱ���
��1���Խ����г���������yԪ��ʾΪ�²���x�ĺ�����
��2�����²���Ϊ���ټ�ʱ���г��������������������Ƕ��٣�
���𰸡���1����������2�����²���x=300��ʱ�����г�������������������Ϊ25000Ԫ
��������
��1������ܳɱ���������=������-�ܳɱ��ɵ����г���������![]() Ԫ���²���
Ԫ���²���![]() �ĺ���ʽ����2����
�ĺ���ʽ����2����![]() ʱ�������䷽������κ��������ֵ25000����
ʱ�������䷽������κ��������ֵ25000����![]() ʱ���ɺ����ĵ����Կɵ�
ʱ���ɺ����ĵ����Կɵ�![]() ���ɴ˵ô𰸣�
���ɴ˵ô𰸣�
�⣺��1�������裬�ܳɱ�Ϊ20000+100x��
��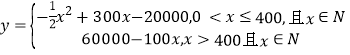 ��
��
��2����0��x��400ʱ��![]() ��
��
��x=300ʱ��ymax=25000��
��x��400ʱ��y=60000��100x�Ǽ�������
��y��60000��100��400=20000��
�൱�²���x=300��ʱ�����г�������������������Ϊ25000Ԫ��

��ϰ��ϵ�д�
�����Ŀ