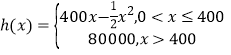题目内容
【题目】已知椭圆
的方程为
，则其长轴长为__________；若
为
的右焦点， 
为
的上顶点， 
为
上位于第一象限内的动点，则四边形
的面积的最大值为__________．
【答案】 
【解析】由题意易得：长轴长为
；
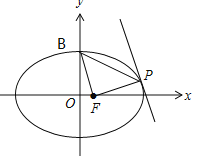
四边形OBPF的面积为三角形OBF与三角形BFP的面积和，
三角形OBF的面积为定值
，要使三角形BFP的面积最大，则P到直线BF的距离最大，
设与直线BF平行的直线方程为y=﹣x+m，
联立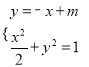
，可得3x2﹣4mx+2m2﹣2=0．
由△=16m2﹣4×3×（2m2﹣2）=0，解得m=
．
∵P为C上位于第一象限的动点，
∴取m=
，此时直线方程为y=﹣x+
．
则两平行线x+y=1与x+y﹣
的距离为d=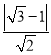
.．
∴三角形BFP的面积最大值为S=
．
∴四边形OAPF（其中O为坐标原点）的面积的最大值是
=
．
故答案为： 
．
练习册系列答案
相关题目
