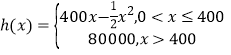ЬтФПФкШн
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФзѓЁЂгвСНИіНЙЕуЗжБ№ЮЊ
ЕФзѓЁЂгвСНИіНЙЕуЗжБ№ЮЊ![]() ЃЌРыаФТЪ
ЃЌРыаФТЪ![]() ЃЌЖЬжсГЄЮЊ2.
ЃЌЖЬжсГЄЮЊ2.
ЃЈЂёЃЉЧѓЭждВЕФЗНГЬЃЛ
ЃЈЂђЃЉЩшЕу![]() ЮЊЭждВЩЯЕФвЛЖЏЕуЃЈЗЧГЄжсЖЫЕуЃЉЃЌ
ЮЊЭждВЩЯЕФвЛЖЏЕуЃЈЗЧГЄжсЖЫЕуЃЉЃЌ![]() ЕФбгГЄЯпгыЭждВНЛгк
ЕФбгГЄЯпгыЭждВНЛгк![]() ЕуЃЌ
ЕуЃЌ![]() ЕФбгГЄЯпгыЭждВНЛгк
ЕФбгГЄЯпгыЭждВНЛгк![]() ЕуЃЌШє
ЕуЃЌШє![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]() ЃЌЧѓжБЯп
ЃЌЧѓжБЯп![]() ЕФЗНГЬ.
ЕФЗНГЬ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ЃЈЂђЃЉ
ЃЈЂђЃЉ![]() Лђ
Лђ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈЂёЃЉгЩЬтвтЕУ![]() ЃЌдйгЩ
ЃЌдйгЩ![]()
![]() ЭждВЕФЗНГЬЮЊ
ЭждВЕФЗНГЬЮЊ![]() ЃЛЃЈЂђЃЉЂйЕБжБЯп
ЃЛЃЈЂђЃЉЂйЕБжБЯп![]() аБТЪВЛДцдкЪБЃЌВЛЗСШЁ
аБТЪВЛДцдкЪБЃЌВЛЗСШЁ![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]() ЃЌВЛЗћКЯЬтвт. ЂкЕБжБЯп
ЃЌВЛЗћКЯЬтвт. ЂкЕБжБЯп![]() аБТЪДцдкЪБЃЌЩшжБЯп
аБТЪДцдкЪБЃЌЩшжБЯп![]() ЃЌ гЩ
ЃЌ гЩ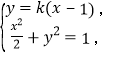
![]() ЕУ
ЕУ![]()
![]()
![]()
![]() ЃЌдйЧѓЕу
ЃЌдйЧѓЕу![]() ЕФжБЯп
ЕФжБЯп![]() ЕФОрРы
ЕФОрРы![]()
![]() Еу
Еу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]()
![]()
![]() Ёр
Ёр![]() Лђ
Лђ![]()
![]() ЫљЧѓЗНГЬЮЊ
ЫљЧѓЗНГЬЮЊ![]() Лђ
Лђ![]() .
.
ЪдЬтНтЮіЃК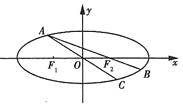
ЃЈЂёЃЉгЩЬтвтЕУ![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
ЁрЭждВЕФЗНГЬЮЊ![]() .
.
ЃЈЂђЃЉЂйЕБжБЯп![]() аБТЪВЛДцдкЪБЃЌВЛЗСШЁ
аБТЪВЛДцдкЪБЃЌВЛЗСШЁ![]() ЃЌ
ЃЌ
Ёр![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]() ЃЌВЛЗћКЯЬтвт.
ЃЌВЛЗћКЯЬтвт.
ЂкЕБжБЯп![]() аБТЪДцдкЪБЃЌЩшжБЯп
аБТЪДцдкЪБЃЌЩшжБЯп![]() ЃЌ
ЃЌ
гЩ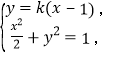 ЛЏМђЕУ
ЛЏМђЕУ![]() ЃЌ
ЃЌ
Щш![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ
ЁпЕу![]() ЕФжБЯп
ЕФжБЯп![]() ЕФОрРы
ЕФОрРы![]() ЃЌ
ЃЌ
гж![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЁрЕу
ЕФжаЕуЃЌЁрЕу![]() ЕНжБЯп
ЕНжБЯп![]() ЕФОрРыЮЊ
ЕФОрРыЮЊ![]() ЃЌ
ЃЌ
Ёр![]() УцЛ§ЮЊ
УцЛ§ЮЊ![]()
![]()
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() Лђ
Лђ![]() ЃЌ
ЃЌ
ЁржБЯп![]() ЕФЗНГЬЮЊ
ЕФЗНГЬЮЊ![]() Лђ
Лђ![]() .
.
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈЂёЃЉЧѓКЏЪ§![]() ЕФЕЅЕїЧјМфгыМЋжЕЃЛ
ЕФЕЅЕїЧјМфгыМЋжЕЃЛ
ЃЈЂђЃЉШє![]() ЃЌЧв
ЃЌЧв![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК ![]() .
.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЕФЕЅЕїдіЧјМфЮЊ
ЕФЕЅЕїдіЧјМфЮЊ![]() ЃЌЕЅЕїМѕЧјМфЮЊ
ЃЌЕЅЕїМѕЧјМфЮЊ![]() ЃЌКЏЪ§
ЃЌКЏЪ§![]() дк
дк![]() ДІШЁЕУМЋДѓжЕ
ДІШЁЕУМЋДѓжЕ![]() ЃЌЧв
ЃЌЧв![]() ЃЛЃЈ2ЃЉМћНтЮі.
ЃЛЃЈ2ЃЉМћНтЮі.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓЕМЪ§ЃЌдйЧѓЕМКЏЪ§СуЕуЃЌСаБэЗжЮіЕМКЏЪ§ЗћКХБфЛЏЙцТЩЃЌНјЖјШЗЖЈЕЅЕїЧјМфвдМАМЋжЕЃЈ2ЃЉЮЊМЋжЕЕуЦЋвЦЮЪЬтЃЌЯШЙЙдьКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌИљОнЕМЪ§ПЩЕУ
ЃЌИљОнЕМЪ§ПЩЕУ![]() ЕЅЕїадЃЌМДЕУ
ЕЅЕїадЃЌМДЕУ![]() ЃЌзюКѓИљОн
ЃЌзюКѓИљОн![]() ЕЅЕїадЕУ
ЕЅЕїадЕУ![]() ЃЌМДжЄЕУНсТл
ЃЌМДжЄЕУНсТл
ЪдЬтНтЮіЃКЃЈЂёЃЉгЩ![]() ЃЌ
ЃЌ
взЕУ![]() ЕФЕЅЕїдіЧјМфЮЊ
ЕФЕЅЕїдіЧјМфЮЊ![]() ЃЌЕЅЕїМѕЧјМфЮЊ
ЃЌЕЅЕїМѕЧјМфЮЊ![]() ЃЌ
ЃЌ
КЏЪ§![]() дк
дк![]() ДІШЁЕУМЋДѓжЕ
ДІШЁЕУМЋДѓжЕ![]() ЃЌЧв
ЃЌЧв![]()
ЃЈЂђЃЉгЩ![]() ЃЌ
ЃЌ ![]() ЃЌВЛЗСЩш
ЃЌВЛЗСЩш![]() ЃЌдђБига
ЃЌдђБига![]() ЃЌ
ЃЌ
ЙЙдьКЏЪ§![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
дђ![]()
![]() ЃЌЫљвд
ЃЌЫљвд![]() дк
дк![]() ЩЯЕЅЕїЕндіЃЌ
ЩЯЕЅЕїЕндіЃЌ ![]() ЃЌвВМД
ЃЌвВМД![]() Жд
Жд![]() КуГЩСЂ.
КуГЩСЂ.
гЩ![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ыљвд![]()
![]()
![]() ЃЌ
ЃЌ
МД![]() ЃЌгжвђЮЊ
ЃЌгжвђЮЊ![]() ЃЌ
ЃЌ ![]() ЃЌЧв
ЃЌЧв![]() дк
дк![]() ЩЯЕЅЕїЕнМѕЃЌ
ЩЯЕЅЕїЕнМѕЃЌ
Ыљвд![]() ЃЌМДжЄ
ЃЌМДжЄ![]() .
.