题目内容
【题目】如图,正三棱柱![]() 所有棱长都是2,D棱AC的中点,E是
所有棱长都是2,D棱AC的中点,E是![]() 棱的中点,AE交
棱的中点,AE交![]() 于点H.
于点H.
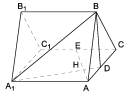
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)参考解析;(2) ![]() ;(3)
;(3) ![]()
【解析】
试题分析:(1)由正三棱柱![]() ,可得平面ACB⊥平面
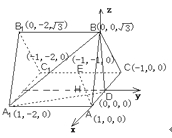
,可得平面ACB⊥平面![]() .又DB⊥AC.所以如图建立空间直角坐标系.分别点A,E,B,D,
.又DB⊥AC.所以如图建立空间直角坐标系.分别点A,E,B,D, ![]() 的坐标,得出相应的向量.即可得到向量AE与向量BD,向量
的坐标,得出相应的向量.即可得到向量AE与向量BD,向量![]() 的数量积为零.即可得直线
的数量积为零.即可得直线![]() 平面
平面![]() .
.
(2)由平面![]() ,平面
,平面![]() 分别求出这两个平面的法向量,根据法向量的夹角得到二面角
分别求出这两个平面的法向量,根据法向量的夹角得到二面角![]() 的余弦值(根据图形取锐角).
的余弦值(根据图形取锐角).
(3)点到平面的距离,转化为直线与法向量的关系,再通过解三角形的知识即可得点到平面的距离.本小题关键是应用解三角形的知识.
试题解析:(1)证明:建立如图所示, ![]()
![]() ∵
∵![]()
![]()
∴![]() 即AE⊥A1D, AE⊥BD
即AE⊥A1D, AE⊥BD
∴AE⊥面A1BD
(2)由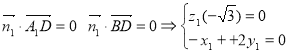 ∴取
∴取![]()
设面AA1B的法向量为 ![]()
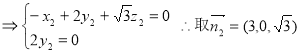 ,
, ![]()
由图可知二面角D—BA1—A的余弦值为 ![]()
(3)![]() ,平面A1BD的法向量取
,平面A1BD的法向量取![]()
则B1到平面A1BD的距离d=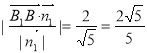

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目