Question

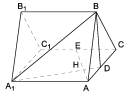
【题目】在直三棱柱中， ,点分别为的中点.

（1）求证： 平面；

（2）求三棱锥的体积（锥体的体积公式，其中为底面面积， 为高）

Answer 1

【答案】（1）见解析（2）

【解析】试题分析：（1）欲证平面，即证MN∥AC′；（2）利用VA′﹣MNC=VN﹣A′MC=VN﹣A′BC=VA′﹣NBC，求三棱锥A′﹣MNC的体积．

试题解析：

（1）

连接AB′，AC′，由已知∠BAC=90°，AB=AC，三棱柱ABC-A′B′C′为直三棱柱，

所以M为AB′的中点，又因为N为B′C′中点，所以MN∥AC′，

又MN平面A′ACC′，AC′平面A′ACC′，所以MN∥平面A′ACC′；

（2）连结BN，由题意A′N⊥B′C′，

∵平面A′B′C′∩平面B′BCC′=B′C′，

∴A′N⊥平面NBC

又A′N=B′C′=1，

故VA′﹣MNC=VN﹣A′MC=VN﹣A′BC=VA′﹣NBC=．