题目内容
6.已知焦点在x轴上的双曲线的离心率为$\sqrt{3}$,虚轴长为2$\sqrt{2}$.(1)求双曲线C的方程;
(2)已知直线x-y+m=0与双曲线C交于不同的两点A,B,若OA⊥OB,求m的值.(O为坐标原点)
分析 (1)设出双曲线的方程,由离心率公式和a,b,c的关系,求得a,b,即可得到所求方程;
(2)联立直线方程和双曲线的方程,消去y,可得x的方程,运用韦达定理和直线垂直的条件,计算即可得到所求m的值.
解答 解:(1)设双曲线的标准方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0),
由题意可得2b=2$\sqrt{2}$,e=$\frac{c}{a}$=$\sqrt{3}$,c2=a2+b2,
解得a=1,b=$\sqrt{2}$,
故双曲线的标准方程为x2-$\frac{{y}^{2}}{2}$=1;
(2)联立直线方程与双曲线方程得:$\left\{\begin{array}{l}{x-y+m=0}\\{2{x}^{2}-{y}^{2}=2}\end{array}\right.$,
消去y,可得x2-2mx-2-m2=0,
判别式△=4m2+4(2+m2)>0,恒成立,
设A(x1,y1),B(x2,y2),
由韦达定理知:x1+x2=2m,x1x2=-2-m2,
由OA⊥OB,可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1x2+y1y2=0,
由y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2,
可得2x1x2+m(x1+x2)+m2=0,
即-2m2-4+2m2+m2=0,解得m=±2,成立.
故m的值为±2.
点评 本题考查双曲线的方程和性质,主要是离心率的运用,考查直线方程和双曲线的方程联立,运用韦达定理,以及两直线垂直的条件,考查运算能力,属于中档题.

练习册系列答案
相关题目
18.如图,将圆沿AB折叠后,圆弧恰好经过圆心,则∠AOB的度数等于( )
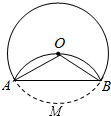

| A. | 60° | B. | 90° | C. | 120° | D. | 150° |
16.执行下面的程序框图,如果输入的t=0.01,则输出的n=( )


| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 7 | D. | $-\frac{5}{a}$ |