题目内容
17.已知中心在原点,焦点在x轴上的双曲线的左右焦点分别记为F1,F2,若P为双曲线的渐近线上一点,若|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=|$\overrightarrow{P{F}_{1}}$-$\overrightarrow{P{F}_{2}}$|,且|PF2|=a(a为实半轴长),求双曲线的离心率$\frac{1+\sqrt{3}}{2}$.分析 运用向量数量积的性质,平方可得$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,即有P在以F1F2为直径的圆上,求得渐近线方程和圆方程,解得交点P,再由条件,结合a,b,c的关系和离心率公式及范围,即可得到所求值.
解答 解:若|$\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$|=|$\overrightarrow{P{F}_{1}}$-$\overrightarrow{P{F}_{2}}$|,
则($\overrightarrow{P{F}_{1}}$+$\overrightarrow{P{F}_{2}}$)2=($\overrightarrow{P{F}_{1}}$-$\overrightarrow{P{F}_{2}}$)2,
化简可得$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
即有P在以F1F2为直径的圆上,
设P(m,n),双曲线的方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,
焦点F1(-c,0),F2(c,0),
联立圆x2+y2=c2,和渐近线方程为y=$\frac{b}{a}$x,
解方程不妨设P(a,b),
由|$\overrightarrow{P{F}_{2}}$|=a,即为(a-c)2+b2=a2,
由a2+b2=c2,e=$\frac{c}{a}$>1,
化简可得2e2-2e-1=0,
解得e=$\frac{1+\sqrt{3}}{2}$,
故双曲线的离心率为$\frac{1+\sqrt{3}}{2}$.
故答案为:$\frac{1+\sqrt{3}}{2}$.
点评 本题考查向量的数量积的性质,考查双曲线的方程和性质,主要是渐近线方程和离心率的求法,属于中档题.

| A. | ($\frac{1}{2}$,5) | B. | ($\frac{1}{2}$,5] | C. | (-∞,5] | D. | ($\frac{1}{2}$,+∞) |
| A. | $A_5^5A_4^2$ | B. | $A_5^5A_5^2$ | C. | $A_5^5A_6^2$ | D. | $A_7^7-4A_6^6$ |
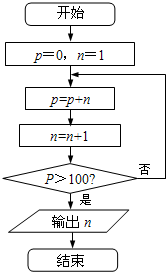
| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
