题目内容
14.设函数f(x)的定义域为A,若存在非零实数t,使得对于任意x∈C(C⊆A),有x+t∈A,且f(x+t)≤f(x),则称f(x)为C上的t低调函数.如果定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且f(x)为[0,+∞)上的10低调函数,那么实数m的取值范围是$[-\sqrt{5}\;,\;\sqrt{5}]$.分析 由已知中t低调函数的定义,结合定义域为[0,+∞)的函数f(x)=-|x-m2|+m2,且 f(x)为[0,+∞)上的10低调函数,构造一个不等式组,结合绝对值的几何意义,将不等式转化为一个关于m的二次不等式,求解不等式得答案.
解答 解:若f(x)为[0,+∞)上的10低调函数,
则当x∈[0,+∞)时,f(x+10)≤f(x),
即-|x+10-m2|+m2≤-|x-m2|+m2
即|x+10-m2|≥|x-m2|,
则m2≤5,
解得m∈[-$\sqrt{5}$,$\sqrt{5}$].
故答案为:[-$\sqrt{5}$,$\sqrt{5}$].
点评 本题考查的知识点是抽象函数及其应用,其中根据已知中t低调函数的定义,构造不等式是解答本题的关键,是中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
2.如图所示某程序框图,则输出的n的值是( )
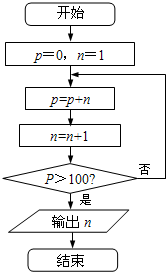

| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
19.若输出k的值为6,则判断框内可填入的条件是( )
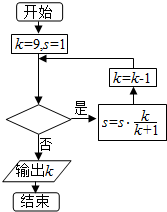

| A. | s>$\frac{1}{2}$ | B. | s>$\frac{3}{5}$ | C. | s>$\frac{7}{10}$ | D. | s>$\frac{4}{5}$ |
3.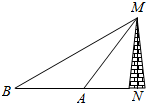 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
 如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )
如图,要测量电视塔的高度,测量者在点A处测得对电视塔的仰角为60°,然后测量者后退200米到点B,测得对电视塔的仰角为30°,则电视塔的高度为( )| A. | 100$\sqrt{2}$m | B. | 100$\sqrt{3}$m | C. | 100m | D. | 200m |