题目内容
18.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个数为( )| A. | 1372 | B. | 2024 | C. | 3136 | D. | 4495 |
分析 分两类,第一类,三点分别在三条边上,第二类,三角形的两个顶点在正方形的一条边上,第三个顶点在另一条边,根据分类计数原理可得.
解答 解:首先注意到三角形的三个顶点不在正方形的同一边上.任选正方形的三边,使三个顶点分别在其上,有4种方法,
再在选出的三条边上各选一点,有73种方法.这类三角形共有4×73=1372个.
另外,若三角形有两个顶点在正方形的一条边上,第三个顶点在另一条边上,则先取一边使其上有三角形的两个顶点,有4种方法,
再在这条边上任取两点有21种方法,然后在其余的21个分点中任取一点作为第三个顶点.这类三角形共有4×21×21=1764个.
综上可知,可得不同三角形的个数为1372+1764=3136.
故选:C.
点评 本题考查了分类计数原理,关键是分类,还要结合几何图形,属于中档题.

练习册系列答案
相关题目
9.已知数列{an}为等差数列,其公差为-2,且a5是a2与a7的等比中项,Sn为{an}(n∈N*)的前n项和,则S8的值为( )
| A. | -104 | B. | -108 | C. | 108 | D. | 104 |
13.已知集合A={x|x2-3x+2<0},B={x|log4x>$\frac{1}{2}$},则( )
| A. | A⊆B | B. | B⊆A | C. | A∩∁RB=R | D. | A∩B=∅ |
5.已知lg2,$lg(sinx-\frac{1}{3})$,lg(1-y)顺次成等差数列,则( )
| A. | y有最大值1,无最小值 | B. | y有最小值-1,最大值1 | ||
| C. | y有最小值$\frac{7}{9}$,无最大值 | D. | y有最小值$\frac{7}{9}$,最大值1 |
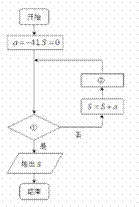 右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.
右图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.①处可填写a>0;②处可填写a=a+2.