题目内容
3. 如图,四棱柱ABCD-A1B1C1D1中,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1,C,D三点的平面记为α,BB1与α的交点为E,F为BC的中点,G在侧棱AA1上,
如图,四棱柱ABCD-A1B1C1D1中,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1,C,D三点的平面记为α,BB1与α的交点为E,F为BC的中点,G在侧棱AA1上,(1)证明:E为BB1的中点,
(2)若AG:A1G=3:1,求证:FG∥平面CDE.
分析 (1)延长DC与AB相交于P,则P?DC,连结A1P交BB1于E,由已知推导出△A1AP∽△BQP,由此能证明E为BB1的中点.
(2)取BE中点M,连结FM、GM,由已知推导出面GFM∥面A1ECD,由此能证明GF∥面CDE.
解答  证明:(1)在底面ABCD中,∵四边形ABCD为梯形,AD∥BC,且AD=2BC,
证明:(1)在底面ABCD中,∵四边形ABCD为梯形,AD∥BC,且AD=2BC,
延长DC与AB相交于P,则P?DC,连结A1P交BB1于E,
∵DC?平面α,∴P?α,
∵AD∥BC,且AD=2BC,∴BC:AD=PB:AP=1:2,
∵A1A∥BQ
∴△A1AP∽△BQP,
∴$\frac{BE}{A{A}_{1}}$=$\frac{BP}{AP}$=2,
∴E为BB1的中点.
(2)取BE中点M,连结FM、GM,
∵F、M为BC、BE中点,∴MF∥EC,
∵${A}_{1}G=\frac{1}{4}{A}_{1}A,EM=\frac{1}{4}{B}_{1}B$,∴A1G$\underset{∥}{=}$EM,∴A1E∥GM,
∴面GFM∥面A1ECD,
∴GF∥面CDE.
点评 本题考查线段中点的证明,考查线面平行的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
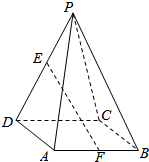 如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为所在边中点,证明:EF∥平面PBC.
如图,四棱锥P-ABCD中,四边形ABCD为平行四边形,E,F分别为所在边中点,证明:EF∥平面PBC.