题目内容
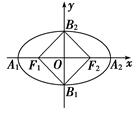
若椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,则椭圆的离心率为 .
 .
.
解析试题分析:因为椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,所以借助于椭圆的对称性,椭圆的离心率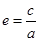 =cos45°=
=cos45°= 。
。
考点:本题主要考查椭圆的几何性质。
点评:简单题,注意到椭圆的离心率即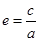 。
。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
题目内容
若椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,则椭圆的离心率为 .
 .
.
解析试题分析:因为椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点,所以借助于椭圆的对称性,椭圆的离心率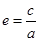 =cos45°=
=cos45°= 。
。
考点:本题主要考查椭圆的几何性质。
点评:简单题,注意到椭圆的离心率即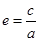 。
。

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案