题目内容
在直角坐标系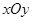 中,点
中,点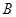 与点
与点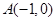 关于原点
关于原点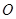 对称.点
对称.点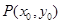 在抛物线
在抛物线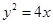 上,且直线
上,且直线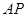 与
与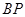 的斜率之积等于-
的斜率之积等于-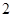 ,则
,则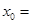 _____________
_____________
 -1
-1
解析试题分析:∵点B与点A(-1,0)关于原点O对称,∴B(1,0).
∴kAP=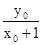 ,kBP=
,kBP=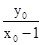 ,
,
∵kAP•kBP=-2,∴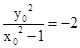 ,
,
又∵点P(x0,y0)在抛物线y2=4x上,∴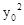 =4x0
=4x0
代入上式得到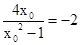 ,化为
,化为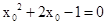 ,解得x0=
,解得x0=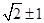 .
.
∴x0= -1.答案为
-1.答案为 -1.
-1.
考点:点对称,直线垂直的条件,抛物线的几何性质,方程组解法。
点评:中档题,熟练掌握中心对称性、斜率的计算公式、点在曲线上即满足曲线的方程解出即可。

练习册系列答案
相关题目
 、
、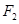 为双曲线C:
为双曲线C: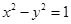 的左、右焦点,点P在C上,
的左、右焦点,点P在C上,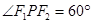 ,则
,则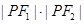 = ;
= ;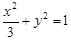 上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 .
上,顶点A是椭圆的一个焦点,且椭圆的另外一个焦点在BC边上,则△ABC的周长是 .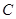 :
: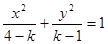 ,给出下面四个命题:
,给出下面四个命题: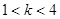 时,曲线
时,曲线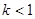 或
或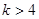 ;
;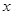 轴上的椭圆,则
轴上的椭圆,则 .
.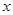 轴上,中心在原点,一条渐进线为
轴上,中心在原点,一条渐进线为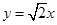 ,点
,点 在双曲线上,则双曲线的标准方程是 .
在双曲线上,则双曲线的标准方程是 .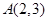 关于直线
关于直线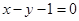 的对称点
的对称点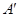 的坐标为 ;
的坐标为 ;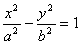
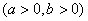 的渐近线与圆
的渐近线与圆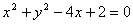 有公共点,则该双曲线的离心率的取值范围是___________.
有公共点,则该双曲线的离心率的取值范围是___________.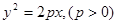 焦点的直线与抛物线交于
焦点的直线与抛物线交于 两点,
两点,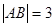 ,且
,且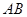 中点的纵坐标为
中点的纵坐标为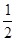 ,则
,则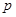 的值为______.
的值为______.