题目内容
11.求椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的顶点、焦点坐标、长轴长及离心率.分析 利用椭圆的方程直接求解顶点、焦点坐标、长轴长及离心率.
解答 解:椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的顶点(±5,0)、(0,±4);焦点坐标(±3,0)、长轴长10,离心率e=$\frac{c}{a}$=$\frac{3}{5}$
点评 本题考查椭圆的简单性质,是基础题.

练习册系列答案
相关题目
3.已知集合A={x∈R|-1<x<1},B={x∈R|(x-2)(x+1)<0},则A∩B=( )
| A. | (0,2) | B. | (-1,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1)∪(0,+∞) |
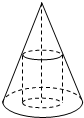 如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.
如图:一个圆锥的底面半径为1,高为3,在其中有一个半径为x的内接圆柱.