Question

【题目】2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示：

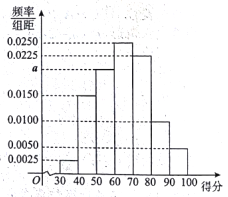
(Ⅰ)估计该组数据的中位数、众数；

(Ⅱ)由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N(μ，210)，μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表)，利用该正态分布，求P(50.5<Z<94)；

(Ⅲ)在(Ⅱ)的条件下，有关部门为此次参加问卷调査的市民制定如下奖励方案：

(i)得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；

(ii)每次赠送的随机话费和对应概率如下：

赠送话费(单元：元)	10	20
概率

现有一位市民要参加此次问卷调查，记X(单位：元)为该市民参加.问卷调查获赠的话费，求X的分布列和数学期望.

附： ，

若ZN(μ，σ2)，则P(μ－σ<Z<μ+σ)= 0.6826，P(μ－2σ<Z<μ+2σ)=0.9544.

Answer 1

【答案】(1) 65，65 (2) 0.8185（3）

【解析】试题分析：(Ⅰ) 由(0.0025 +0.0050+0.0100+0.0150 + a + 0. 0225 + 0. 0250)×10 =1，得a =0.0200,设中位数为，由(0.0025 + 0. 0150 + ) ×10+(x-60) ×0.0250 = 0.5000，解得x = 65, 由频率分布直方图可知众数为65.

(Ⅱ) 从这1000人问卷调查得到的平均值μ为

μ= 35×0.025 + 45×0.15 +55×0.20+65×0.25+75×0.225+85×0.1+ 95×0.05=65，因为由于得分Z服从正态分布N(65,210)，所以

P(50.5<Z<94)=P(60-14.5<Z<60 + 14.5×2)= 即得解;

(Ⅲ) 设得分不低于μ分的概率为p，则P(Z≥μ)= ，由题意得各概率即可得分布列和期望.

试题解析：

(Ⅰ)由(0.0025 +0.0050+0.0100+0.0150 + a + 0. 0225 + 0. 0250)×10 =1，得a =0.0200,

设中位数为，由(0.0025 + 0. 0150 + ) ×10+(x-60) ×0.0250 = 0.5000，解得x = 65,

由频率分布直方图可知众数为65.

(Ⅱ)从这1000人问卷调查得到的平均值μ为

μ= 35×0.025 + 45×0.15 +55×0.20+65×0.25+75×0.225+85×0.1+ 95×0.05

=0.875 + 6.75+11 +16.25+ 16. 875 + 8.5 +4.75 = 65

因为由于得分Z服从正态分布N(65,210)，

所以P(50.5<Z<94)=P(60-14.5<Z<60 + 14.5×2)= =0.8185.

(Ⅲ)设得分不低于μ分的概率为p，则P(Z≥μ)= ，

X的取值为10,20,30,40，

P(X=10) =，

P(X=30) =，.

所以X的分布列为：

X	10	20	30	40

所以.