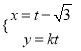题目内容
【题目】已知圆
，圆
内一定点
，动圆
过点
且与圆内切.记动圆圆心的轨迹为
.
（Ⅰ）求轨迹方程；
（II）过点
的动直线l交轨迹于M，N两点，试问：在坐标平面上是否存在一个定点Q，使得以线段MN为直径的圆恒过点Q？若存在，求出点Q的坐标；若不存在，请说明理由.
【答案】(I) 
；(II)存在，恒过点Q(0，1).
【解析】
（Ⅰ）由题意可知：
，P点轨迹是以A、B为焦点的椭圆，即可求得椭圆的标准方程；
（Ⅱ）利用特例先确定定点Q，再推广到一般情况即可.
解:（Ⅰ）解：设动圆圆心
，半径为
.
，
故点
的轨迹为椭圆，
，
，
故圆心的轨迹方程为
(II)当l与x轴平行时，以线段MN为直径的圆的方程为x2＋
＝
；
当l与y轴平行时，以线段MN为直径的圆的方程为x2＋y2＝1.
由
得
故若存在定点Q，则Q的坐标只可能为Q(0，1).
下面证明Q(0，1)为所求：
若直线l的斜率不存在，上述已经证明.
若直线l的斜率存在，设直线l：y＝kx－
，
M(x1，y1)，N(x2，y2)，
由
得(9＋18k2)x2－12kx－16＝0，
Δ＝144k2＋64(9＋18k2)＞0，
x1＋x2＝
，x1x2＝
，
＝(x1，y1－1)，
＝(x2，y2－1)，
＝x1x2＋(y1－1)(y2－1)
＝(1＋k2)x1x2－
(x1＋x2)＋
＝(1＋k2)·
－·
＋＝0，
∴⊥，即以线段MN为直径的圆恒过点Q(0，1).
启东小题作业本系列答案
【题目】2017年是某市大力推进居民生活垃圾分类的关键一年，有关部门为宣传垃圾分类知识，面向该市市民进行了一次“垃圾分类知识”的网络问卷调查，每位市民仅有一次参与机会，通过抽样，得到参与问卷调查中的1000人的得分数据，其频率分布直方图如图所示：
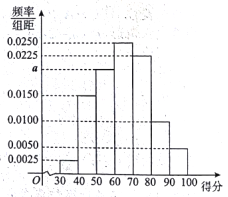
(Ⅰ)估计该组数据的中位数、众数；
(Ⅱ)由频率分布直方图可以认为，此次问卷调查的得分Z服从正态分布N(μ，210)，μ近似为这1000人得分的平均值(同一组数据用该区间的中点值作代表)，利用该正态分布，求P(50.5<Z<94)；
(Ⅲ)在(Ⅱ)的条件下，有关部门为此次参加问卷调査的市民制定如下奖励方案：
(i)得分不低于μ可获赠2次随机话费，得分低于μ则只有1次；
(ii)每次赠送的随机话费和对应概率如下：
赠送话费(单元：元) | 10 | 20 |
概率 |
|
|
现有一位市民要参加此次问卷调查，记X(单位：元)为该市民参加.问卷调查获赠的话费，求X的分布列和数学期望.
附： 
，
若ZN(μ，σ2)，则P(μ－σ<Z<μ+σ)= 0.6826，P(μ－2σ<Z<μ+2σ)=0.9544.
